Abstract
Identifying the most influential spreaders as an influence maximization problem (IMP) has become one of the most compelling topics in social network analysis due to its successes in viral marketing. In this paper, we first assume the network model to be a multiplex network, consisting of layers where each layer represents a different type of association among users based on their activities. We then define the concept of the maximum independent set (MIS) problem within multiplex networks. Next, we propose MIS as a potential solution to the MIP for identifying the initial candidate set of spreaders. Finally, we develop a learning automaton framework to solve the MIS in multiplex networks and to demonstrate its applicability for influence maximization. Theoretical properties of the MIS in multiplex networks are provided, along with various experiments on both artificial and real networks to showcase the performance of the proposed algorithm.
Introduction
Information diffusion through online user spreaders in social networks is a captivating phenomenon that attracts attention from both social scientists and computer scientists. This process, which involves the propagation of information from influential users to others within the network, serves as a focal point in social network analysis and motivates the development of intelligent algorithms. Understanding how information spreads and influences users’ behavior has implications for various domains, including marketing strategies, public health campaigns, and online content moderation. Therefore, investigating the dynamics of information diffusion in social networks is crucial for comprehending the underlying mechanisms shaping user interactions and network dynamics. Identifying a limited number of key users or influential users as initial spreaders with a high ability to affect the thoughts, attitudes, beliefs, or behaviors of others within the network as much as possible is also can be known as an influence maximization problem1,2. In recent years, many scholars have tried to investigate the influence maximization on a standard and conventional network model (e.g., binary network) with a single-layer network that reflects one type of user activity, such as friendship. However, modeling a social network with different types of user activities using a single layer cannot take into consideration real scenarios that occur in real context due to several types of activities of users in a social network, such as posting, liking, commenting, and sharing content or similar activities in some social networks simultaneously3.
In real-world scenario4, individuals often engage in multifaceted interactions across different social platforms, each serving as a distinct layer of influence within a multilayer network. For instance, consider a marketing campaign where users share an advertisement on Facebook to inform their friends and persuade them to purchase a product. Simultaneously, these users may share the same advertisement with a different set of friends on Instagram or promote an upcoming event through professional networks like LinkedIn. In such cases, relying solely on a single-layer network model overlooks critical aspects of influence propagation that occur across different layers of interaction. By adopting a multiplex network framework, which captures the interconnectedness and diversity of interactions across various social platforms, we gain a more comprehensive understanding of the dynamics of influence diffusion. This approach enables us to account for the nuanced ways in which individuals influence and are influenced across multiple layers of social interaction, thereby facilitating more accurate and effective strategies for influence maximization.
The multifaceted interactions observed in real-world scenarios underscore the need for advanced network models capable of capturing the diversity and complexity of relationships across different contexts. Single-layer networks often fall short of representing the interconnected nature of these systems, whereas multiplex and multilayer networks provide robust frameworks to bridge this gap. These models go beyond single-layer representations by incorporating multiple layers of interactions, with each layer corresponding to a specific type of relationship or influence. Multiplex networks focus on distinct relationships among the same set of nodes across various layers, such as interactions on different social platforms. In contrast, multilayer networks offer a broader perspective, capturing not only structural relationships but also dynamic processes and functional variations across layers. By leveraging the complementary strengths of both models, researchers can better analyze the propagation of influence and the adhesion of nodes across complex systems, facilitating a deeper understanding of how diverse interactions shape connectivity and influence diffusion. Consequently, studying these networks requires a detailed analysis of the relationships and interactions between different layers or types of nodes to fully capture their complexity. Thus such networks can be modeled as multiplex networks and also multilayer networks3,5,6,7. We note that multilayer and multiplex networks are employed to model complex systems with different interactions, albeit possessing distinct features. Both network types consist of multiple layers, each signifying diverse relationships or interactions among nodes. Nodes and edges can traverse multiple layers, facilitating layer overlap and interlayer connectivity. These networks intricately represent the complexities of real-world systems. However, they diverge in their representation and focus. Multiplex networks delineate different relationships among the same node set, like social interactions. Conversely, multilayer networks encapsulate diverse interaction aspects, such as temporal or spatial variations. While each layer in multiplex networks usually depicts a distinct structural relationship, multilayer networks incorporate both structural and functional layers. Furthermore, multiplex networks typically capture static relationships, whereas multilayer networks excel in modeling dynamic processes and heterogeneous interactions.
Most studies8,9,10 have focused on influential nodes in single isolated networks and may not be able to address leading nodes as influencers in more complex multilayer networks (i.e., multiplex networks). But, in real-world scenarios, nodes frequently engage in multifaceted interactions across various social platforms, each representing a distinct layer of influence within a multilayer network. The primary advantage of multilayer networks lies in their capacity to provide a more general and flexible modeling framework compared to multiplex networks, as they encapsulate the complexity of diverse interactions while offering a richer representation of social dynamics. For example, different layers in a multilayer network can correspond to distinct social media platforms such as Facebook, X, TikTok, and Instagram, allowing researchers to accurately portray situations where individuals may actively participate in some platforms while remaining inactive in others. This fine-grain representation is crucial for understanding the complexities of social interactions in today’s digital age, as it enables differentiation between nodes that are absent from a specific platform and those that lack relationships within that platform. In a multiplex network, where every node must exist in all layers, such distinctions are lost. Furthermore, this flexibility becomes particularly relevant in the context of the Maximum Independent Set (MIS) algorithm, as nodes that are not connected in a particular layer can still be included in the MIS without being artificially constrained by the requirement to be present in all layers. The advantage of multilayer networks lies in their ability to serve as a more general and flexible modeling framework compared to multiplex networks, as they encapsulate the complexity of various types of interactions while allowing for a richer representation of social dynamics. In a multilayer network, different layers can represent distinct social media platforms enabling researchers to accurately depict scenarios where individuals may engage with some platforms while remaining inactive on others. This is particularly significant because, in a multiplex network, every node must be present in all layers, which creates limitations in distinguishing between nodes that are absent from a specific platform and those that simply lack relationships within that platform. For instance, an individual who does not have a Facebook account can still interact with others on TikTok and Instagram, and this nuanced representation is vital for understanding the complexities of social interactions in today’s digital age. While the implications of this distinction might not be critical for certain processes, such as spreading mechanisms discussed in the paper, they become highly relevant in the context of the MIS algorithm. In the case of multilayer networks, nodes that are not connected in a particular layer can still be included in the MIS because they are not artificially constrained by the requirement of being present in all layers. This flexibility allows for more accurate identification of independent sets, as it acknowledges that nodes not involved in specific interactions can still play a role in the overall network structure. Therefore, multilayer networks not only enhance the fidelity of social network modeling but also provide a robust framework for analyzing complex interdependencies and dynamics, ultimately leading to better insights and practical applications in understanding social behaviors and relationships present in all layers. This allows for more accurate identification of independent sets, acknowledging the role of nodes not involved in specific interactions within the overall network structure. For instance, in a marketing campaign where users share an advertisement on Facebook to inform friends while simultaneously promoting the same advertisement on Instagram or an event on LinkedIn, a single-layer network model would overlook critical aspects of influence propagation across these various interactions. By adopting a multilayer network framework, we gain a comprehensive understanding of the dynamics of influence diffusion, accounting for the intricate ways individuals influence and are influenced across multiple layers of social interaction. This approach ultimately facilitates the development of more accurate and effective strategies for influence maximization, enhancing our insights into social behaviors and relationships.
In this paper, our emphasis lies in investigating the MIS within multiplex networks, specifically examining their role as influential spreaders within such network structures. The application of the MIS in influence maximization involves identifying a subset of nodes in a network that maximizes the spread of influence or information. In this context, the maximum independent set represents a set of nodes that do not directly influence each other, thereby maximizing the potential reach of influence within the network. By selecting nodes from the maximum independent set as influencers or seed nodes, one can strategically initiate the dissemination of information or influence in such a way that it spreads efficiently throughout the network. This approach helps optimize the selection of initial influencers to maximize the overall impact or reach of a campaign, marketing strategy, or any other process reliant on network diffusion. More clearly, the applicability of the MIS as an initial candidate for spreading in multiplex networks. This leads to a new definition of MIS in multiplex networks, as well as a new algorithm for solving the MIS in multiplex networks. Based on the promising abilities of learning automata (LA) theory1,11 for solving many complex problems in an unknown environment, a new LA-based algorithm is also proposed for finding the MIS in multiplex networks with the largest cardinality.
In the subsequent sections of this paper, we outline the following content: “Related works” section offers a concise review of pertinent literature and foundational concepts relevant to our study. “Preliminaries” section delivers a succinct explanation of the LA theory. In “Proposed algorithm” section, we introduce an LA-based algorithm designed to identify the maximum independent set, while “Complexity analysis” section presents simulation outcomes related to the maximum independent set, with a specific focus on influence maximization discussed in “Experimental results for MISM” section. The final section concludes the paper and reflects on potential avenues for future research.
Related works
Several studies related to information diffusion and influence maximization in social networks are presented to cover a range of topics that can be categorized as including (1) investigating the importance of identifying influential nodes, (2) the development of novel algorithms for influence maximization with new assumptions and their impacts, (3) the exploration of stochastic diffusion models for information diffusion considering uncertainty and variability in the real world and (4) the significance of network controllability in different types of network models. In the remainder of this section, a summary of recent studies is provided.
In12, the authors discussed the study of models describing how ideas and influence spread through social networks, spanning various domains such as medical and technological innovations, game theory, and viral marketing. It introduces the fundamental algorithmic problem posed by Domingos and Richardson regarding the identification of influential individuals to trigger the widespread adoption of innovations. They highlighted the NP-hardness of this optimization problem and presented the first approximation guarantees for efficient algorithms. Using a framework based on submodular functions, they demonstrated that a greedy strategy achieves solutions within 63% of optimal for several model classes, providing a general approach for analyzing algorithm performance in influence problems. Additionally, computational experiments on large collaboration networks show that these approximation algorithms outperform traditional node-selection heuristics like degree and distance centrality. One crucial aspect of infection propagation within multilayer networks is its potential to traverse from one layer to another. Spreading processes typically occur in three distinct scenarios: first, same-node inter-layer transmission, where the infection moves across layers while remaining on the same node, such as when an infected person travels from one city to another. Second, other-node inter-layer transmission, which involves the infection spreading to a different node in another layer, is exemplified by the transmission of disease among individuals from various age groups through direct contact. The third scenario is characterized by other-node intra-layer transmission, where the infection propagates within the same community. In the context of interacting spreading processes in multilayer networks, two types of thresholds have recently been identified: the survival threshold, which determines whether the infection will persist, and the absolute-dominance threshold, which indicates the potential for one process to completely replace another that is occurring simultaneously13.
In14 the authors discussed the significance of selecting seed nodes, which are influential in spreading information across networks. Influence maximization (IM) has been the focus of considerable research within the context of single-layer networks; however, its relevance to multilayer networks is increasingly recognized. The task of pinpointing influential nodes in multilayer networks presents significant challenges and remains relatively underexplored. To tackle this issue, the authors introduced a Community-Based Influence Maximization (CBIM) model. This model utilizes a two-phase methodology: initially, it identifies small communities through a dice neighborhood similarity function and subsequently merges these communities to improve their overall quality. Following this, the model calculates the Edge Weight Sum (EWS) for nodes within each community and employs a quota-based strategy to select seed nodes. Comparative analyses indicate that CBIM surpasses existing IM algorithms, as evidenced by simulations conducted on real-world datasets across various scenarios. In15, the authors examine the significance of identifying influential users within a network to facilitate effective information dissemination, particularly in the realms of viral marketing and brand communication. They present IM as a strategy aimed at pinpointing a select group of key users capable of enhancing the spread of influence. While numerous existing algorithms concentrate on IM within single-layer networks, there is an increasing interest in exploring IM within multilayer networks, spurred by the proliferation of online social networks. The investigation into the K + + Shell decomposition algorithm for detecting influential nodes in multilayer networks is motivated by its ability to prune nodes based on their degree and allocate reward points to their adjacent nodes. A comparative analysis of various IM algorithms reveals that the K + + Shell decomposition algorithm outperforms its counterparts on real-time datasets across diverse settings and environments.
Erlandsson et al.16 focused on information spreading within online social media networks. The research investigates how various seed selection strategies influence spreading dynamics, which are modeled through the independent cascade framework across eighteen multilayer social networks. Of these networks, fifteen are derived from user interaction data collected from public Facebook pages, whereas the other three consist of multilayer networks obtained from a public repository, including two that originate from X (Formerly Twitter). The findings suggest that traditional seed selection strategies, such as K-Shell or VoteRank, commonly used in single-layer networks, may not be effective in multilayer networks. Instead, Degree Centrality emerges as a superior alternative in this context. In17 addresses Influence Maximization (IM), as a significant problem in information diffusion research, which involves selecting a subset of users from a social network to maximize the spread of influence. Despite its importance, there is limited research on IM for multilayer networks, and existing studies often rely on greedy algorithms that provide limited insights. To address this gap, the review emphasizes the examination of the Influence Maximization Problem (IMP) within multilayer networks. It presents innovative concepts such as pairwise reciprocal length and pairwise influence, framing IM as a multi-objective optimization challenge. The Non-dominated Sorting Genetic Algorithm II (NSGA-II) is employed to identify a collection of Pareto-optimal solutions. To improve both diversity and convergence, a heuristic strategy for population initialization and an effective two-point crossover mechanism is utilized. Comprehensive experiments reveal that the presented method exhibits competitive performance regarding influence spread and execution time when compared to existing IM algorithms.
In18, the authors examined the critical role of identifying influential nodes within complex networks, with a particular emphasis on the dynamics of information dissemination in social networks. While traditional influence maximization research predominantly addresses monolayer networks, there is an increasing necessity to broaden this inquiry to encompass multilayer networks, reflecting the growing prevalence of social networks. Nevertheless, the task of pinpointing influential nodes in multilayer networks presents significant challenges and remains relatively under-researched. The authors provide experimental findings that underscore the importance of nodes exhibiting robust connections across both interlayer and intra-layer dimensions. A comparative analysis of various influence maximization algorithms tailored for multilayer networks is presented, informed by these findings. Furthermore, the authors introduce a novel algorithm termed clique-based influence maximization (CIM), designed to enhance the spread of influence by integrating considerations of both interlayer and intra-layer connections.
In19, the authors highlighted the growing importance of online social networks across a range of academic fields and industries, including computer science, sociology, mathematics, information studies, biology, and business. Social network analysis (SNA) is essential for comprehending social relationships and networks, with research concentrating on topics such as information dissemination, influence analysis, and link prediction. Nonetheless, significant research challenges remain, particularly regarding privacy concerns within online social networks. To address these issues, they present a survey of SNA methodologies, visualization techniques, structural analysis, privacy considerations, and practical applications. It commences with fundamental concepts related to network representation and structure, subsequently exploring more sophisticated applications and methodologies. Additionally, a comparative review of recent advancements in SNA challenges is included, alongside a discussion on privacy preservation and prospective research avenues, to assist researchers in their future work.
Wang et al.20 emphasize the critical nature of the influence maximization problem, which involves the selection of influential nodes to enhance their impact within both single-layer and multilayer networks, with particular relevance to marketing and social dynamics. While earlier research has predominantly concentrated on single-layer networks, there is a growing recognition of the necessity to investigate robust influence maximization within multilayer networks. To fill this research void, the authors propose a performance metric designed to evaluate seed influence in multilayer networks amidst structural disruptions. They introduce the MA-RIM algorithm, which incorporates problem-specific operators to effectively identify influential and resilient seeds. The algorithm exhibits competitive performance across both synthetic and real-world networks. Additionally, the study explores how structural alterations affect seed performance, underscoring the efficacy of topological rewiring in amplifying seed influence. In summary, this research illuminates the potential of multilayer networks for advancing the understanding of influence maximization and for pinpointing critical nodes essential for social propagation and information diffusion initiatives. In21, the authors delve into the extensive review of the literature concerning the dynamics of information diffusion within networked systems, conceptualizing the critical task of seed selection as an influence maximization challenge. A variety of effective diffusion models and methodologies have been established to pinpoint influential seeds in both single-layer and multilayer networks. Recent research has highlighted the significance of resilient seeds in the face of structural disruptions in real-world applications. Nevertheless, current strategies for robust influence maximization often lack a generalizable framework and fail to consider diverse scenarios. To overcome these shortcomings, the authors propose a multitasking optimization strategy for seed selection in multilayer networks. This innovative approach simultaneously addresses multiple optimization scenarios and capitalizes on the interconnections among them throughout the search process. They introduce a multi-factorial evolutionary algorithm, MFEA-RIM, which integrates problem-specific operators and prioritizes the structural characteristics of the network during the local refinement phase.
Current research on information diffusion in online social networks reveals a notable gap, as highlighted in22. The existing models predominantly exhibit a deterministic framework, which fails to adequately account for the uncertainty and variability that characterize real-world social networks. To handle this shortcoming, the authors propose the use of stochastic graphs as a more suitable model for social network applications, wherein link weights are conceptualized as random variables. The diffusion model they introduce is grounded in this stochastic graph framework, integrating unknown random variables to denote the influence probabilities linked to these connections. Furthermore, a methodology is established to estimate these influence probabilities through a set of learning automata that are integrated within the diffusion model, allowing for sampling from the links of the stochastic graph. In reference23, the concept of multilayer networks is presented as a complex representation of various real-world systems, characterized by multiple interaction types among nodes. These networks play a crucial role in modeling processes such as influence dissemination, where individuals within a social system propagate influence via contact, communication, or persuasion. Given the critical nature of influence dissemination, researchers are investigating optimal strategies for initiator selection within social networks to enhance its effectiveness.
Sadaf et al.24 ongoing investigations aimed at identifying key nodes that can optimize the spread of influence within complex networks. They propose an innovative methodology that integrates driver node selection techniques from network control theory with a divide-and-conquer approach that capitalizes on community structures. The study delves into the relatively recent idea of utilizing driver nodes situated within communities as seed nodes. The findings suggest that leveraging community structures significantly enhances the effectiveness of the resulting seed sets, indicating a promising avenue for influence maximization methodologies. Additionally, the authors introduce a comprehensive framework for evaluating the controllability of multiplex networks, classifying them into two primary categories: multiple-relation networks and multiple-layer networks characterized by interlayer connections. Their analysis reveals that in multiple-relation networks, a specific layer plays a crucial role in determining the overall controllability of the network, whereas in multiple-layer networks, a limited number of interconnections can greatly improve controllability.
Menichetti et al.25, investigated the theoretical aspects of network controllability, emphasizing its significance in a variety of fields. While earlier research has primarily concentrated on single-layer networks, it is important to note that most complex systems are structured as multilayer networks. The authors present a theoretical framework for examining the linear controllability of these multilayer networks, framing the issue as a combinatorial matching challenge. Their findings indicate that the correlation of external signals across different layers can greatly influence the resilience of multiplex networks against node removal, resulting in a hybrid phase transition within interacting Poisson networks. Furthermore, they demonstrate that multilayer networks can achieve stable fully controllable configurations, even in cases where the individual networks do not maintain full controllability.
Reference26, addresses the complexities associated with managing multilayer networks, especially those functioning across varying timescales. The focus is on two-layer multiplex networks characterized by one-to-one interlayer coupling, examining control strategies when the control signal is directed at a single layer. The research formulates a theoretical framework utilizing disjoint path covers to ascertain the minimum number of inputs required for comprehensive control. The findings indicate that the ability to control is influenced by the disparity in timescales between the layers, with improved controllability observed when the controller engages with the more rapid layer. However, once a certain threshold of timescale difference is surpassed, the requisite number of inputs stabilizes and is dictated by the faster layer. In contrast, exerting control over the slower layer becomes progressively more challenging as the timescale separation increases. The critical threshold for achieving controllability is significantly shaped by the structural characteristics of both layers. By clarifying the interplay between timescale differences and controllability, this study offers valuable insights into the management of complex systems that are subject to various complexities.
Reference27, explores the controllability of multilayer networked sampled-data systems characterized by inter-layer couplings, utilizing zero-order holders (ZOHs) within the control and transmission pathways. The research assesses how both single-rate and multi-rate sampling affect the controllability of multilayer networked linear time-invariant (LTI) systems, establishing sufficient and/or necessary conditions for controllability. The findings indicate that the network architecture and inter-layer couplings can alleviate adverse sampling effects in single-node systems under certain circumstances. The study further investigates the drive-response inter-layer coupling mode, demonstrating that such couplings can enable the overall system to achieve controllability, even when the response layer itself is uncontrollable. Simulations illustrate that modifications to the sampling rate on local channels can produce either beneficial or detrimental impacts on the system’s controllability. In summary, the results indicate that the controllability of multilayer networked sampled-data systems is shaped by interrelated factors. Srivastava et al.28 investigate the intricate relationship between the structural characteristics and control dynamics of complex systems modeled as multilayer networks. The research focuses on how the layered architecture of a system affects its responsiveness, particularly under conditions where control signals are restricted to a single input layer. Utilizing principles from linear control theory, the authors analyze the control dynamics of a duplex network featuring directed interlayer connections. They derive an expression for optimal control energy that takes into account the spectral properties of the layers and the alignment of eigenmodes between the input and target layers. Through the examination of various numerically simulated duplex networks, the study assesses the impact of target-layer densities and layer topologies on control dynamics. A significant finding is that the alignment of layer eigenmodes plays a pivotal role in determining the routing of optimal control energy. Additionally, the research introduces metrics to quantify the routing of optimal control energy across the eigenmodes of each layer. The results contribute valuable insights into the relationship between structure and control in duplex networks, providing a foundation for the development of effective interlayer control strategies in future research.
In29 addresses the target controllability problem in multiplex networks, aiming to maximize the dimension of the controllable subspace. It introduces two variations of the problem: the maximum-cost target controllability problem and the minimum-cost target controllability problem. The former seeks to maximize the covered nodes set, while the latter aims to minimize it along with the driver node-set. To tackle these challenges, the article transforms them into a minimum-cost maximum-flow problem using graph theory. It proposes an algorithm called target minimum-cost maximum-flow (TMM), demonstrating its efficacy in ensuring the control of target nodes with the minimum number of inputs while maximizing or minimizing the covered nodes set. Simulation results on various network models, including Erdos-Rényi and scale-free networks, as well as real-life networks, validate the effectiveness of the TMM algorithm. In30 evaluates different centrality-based seed selection methods for the Budget-Constrained Influence Maximization Problem in multilayer networks under the Multilayer Linear Threshold Model. The research first generalizes three existing metrics—K-shell Decomposition, PageRank, and VoteRank—for application in multilayer networks. Additionally, methods such as Community Based Influence Maximization, Clique Influence Maximization, and K + + Shell have been adapted to focus on influence maximization based on actors rather than nodes. A novel method, Neighbourhood Size Discount, is also introduced. In total, fourteen methods, including a greedy routine and a random choice for comparison, were assessed for their effectiveness. The evaluation encompasses both quantitative and qualitative analyses, providing insights into the performance of these heuristics. A new effectiveness measure, termed “Gain,” considers seed set size, while effectiveness curves are used to delineate the parameters affecting diffusion effectiveness. The study concludes that multiple factors—including internal parameters of the Multilayer Linear Threshold Model, network type, budget, and seed selection method—impact the overall success of influence maximization. Notably, no single seed selection method consistently outperforms others, except for the random choice and greedy approaches, which exhibit distinct performance characteristics. The preliminary assessment across ten networks identifies Degree Centrality Discount, Neighbourhood Size Discount, PageRank (p-rnk variant), and VoteRank (both v-rank and v-rnk-m variants) as the top-performing methods. Further analysis on larger graphs highlights v-rnk-m as the most effective approach. The node-wise ranking (:(p-rnk)) was derived by applying the PageRank algorithm, as originally introduced by Page et al.31, to each layer of the network. Subsequently, a final ranking list was generated by ordering the actors based on their average position across the layer rankings. In the second implementation, referred to as (:p-rnk-m), the original PageRank algorithm was adapted to suit the specific context of this study. This adaptation involved condensing the multilayer network into a single-layer graph to ensure that all actors were retained. Edges were established between actors if at least one layer of the original network contained a connection between them. The output of the PageRank algorithm applied to this condensed network resulted in a comprehensive final ranking list. The concept introduced in32 posits that when an individual A supports another individual B, A’s capacity to support additional individuals typically diminishes. Building on this idea, a vote-based method for identifying influential spreaders, termed VoteRank, is proposed. VoteRank operates by sequentially selecting spreaders based on voting scores assigned to nodes by their neighbors. To determine the top (:r) influential spreaders, each node participates in (:r) voting rounds, with the node receiving the highest votes in each round being designated as the most influential and elected as one of the top (:r) spreaders. Once elected, a node no longer participates in subsequent voting, and the voting influence of its neighbors is also diminished. This mechanism enhances the propagation range when neighboring nodes are elected as spreaders, as the elected node can relay information to them. Therefore, selecting geographically or structurally distant nodes is advantageous, as it maximizes their overall impact on the network. Consequently, the selection probability of a node’s neighbors decreases after it is elected, ensuring that the chosen spreaders are well-dispersed and significant within their local contexts.
Preliminaries
This section aims to furnish foundational information pertinent to the subsequent parts of the paper by succinctly elucidating the maximum independent set problem and its relevance to influence maximization, multiplex networks, and independent sets within multiplex networks, as introduced in this study, alongside the concept of learning automata.
Maximum independent set (MIS)
Let (:G=left(V,:Eright)) represent an undirected graph, where (:V) denotes the set of vertices and (:Ein:Vtimes:V) signifies the set of edges. A subset of vertices, (:Isubseteq:V) qualifies as an independent set (IS) if no edges connect any two vertices within (:I). The maximum independent set (MIS) of graph (:G) is defined as the independent set that possesses the largest cardinality among all independent sets in (:G). The problem of determining the MIS classified as NP-hard prompts the development of various heuristic algorithms aimed at identifying near-optimal solutions. Furthermore, the MIS problem finds applications across multiple scientific disciplines33,34,35,36. For instance, in the context of online social networks, the MIS of users represents clusters of individuals who do not have connections with one another, thereby enhancing resilience against failures.
A useful review of the literature for solving the maximum independent set problem is presented by37. Kaminski et al.38 have explored the reconfigurability of independent datasets in graphs. They propose three models, token jumping, token sliding, and token removal and addition. The token jumping, addition, and removal models are equivalent. Also, proof that based on the tree models, the IS complexity in perfect graphs. Wu et al.39 used an independent set for coloring application in a large graph. The algorithm extracts large independent sets from the network in the preprocessing, and then a memetic algorithm is utilized to color the remaining graph. Each preprocessing application recognizes, with a customized tabu search algorithm, several pairwise distinct ISs of a given size to maximize the vertices removed from the graph.
Balaji et al.40 proposed a simple algorithm by reducing vertex cover. They show that the algorithm can reduce computational time efficiently. Bazgan et al.41 studied the MIS in the network as a vital node whose removal reduces the maximum weight of ISs. They also present a problem as a complementary called minimum node blocker independent set, which is composed of extracting a subset of nodes with a minimum size so that the maximum weight of independent sets in the residual graph does not exceed a prescribed value. In addition, the effectiveness of the algorithm is studied. Theo McKenzie et al.42 proposed a new semi-random model, which chooses a network with a planted IS of size (:k). Their purpose is to provide an adversary with the ability to transform a large number of edges. An adversary may insert edges from the IS to its complement into the subgraph induced by the complement of the IS.
Chalupa et al.43 studied the growth of IS in scale-free networks. It has been demonstrated that the size of a large IS scales linearly with graph size when the graph is large enough. Because the MIS problem is NP-hard, scholars have focused their attention on heuristic algorithms for solving it. Taranenko et al.44 proposed a genetic algorithm (GA) with an elitist approach to solving the MIS problem. To detect the independent set, the algorithm uses a permutation encoding with greedy decoding combined with an elitist approach. A genetic algorithm solution is also suggested by Liu et al.45. To determine the MIS, they used a simple permutation encoding process combined with greedy decoding.
Mehrabi et al.46 have suggested a new GA by introducing a new heuristic called independent crossover, which is applied to guarantee that new offspring are valid after mutation. An algorithm based on ant colony optimization was proposed by Li et al.47. By proposing a complement construction to scatter the search points in search space, they have introduced a new method for obtaining heuristic information and enhanced the solution construction process. The maximum weight independent set (MWIS) problem is addressed by Nogueira et al. using a hybrid iterated local search (ILS) algorithm48. To find the MWIS algorithm, they proposed new neighborhood structures and a reactive perturbation mechanism that dynamically alters the balance between diversification and intensification over time.
The maximum independent set can be applied in influence maximization as an initial spreader in social networks. The finding of influential nodes as spreaders in complex social networks, after a study as reported in49, focuses on the concept of ‘network decomposition’ using concepts such as the k-shell and k-truss50, and onion decomposition51. All these methods are iterative and, therefore, slow; hence, they need information on global network connectivity. It seems that they are also proper spreaders to locate highly connected nodes. It has been shown that a centrality measure, such as the shortest-path betweenness centrality, is an effective method for finding influential spreaders. However, this approach has the same drawbacks as their equivalents for single-layer networks, as outlined in52. Moreover, another centrality measure, closeness, and betweenness have very high computational complexity. Therefore, it is not appropriate to use real multiplex social networks. The authors of53 proposed a PageRank centrality for multilayer networks, which requires an artificial order among the layers of the networks, making it far from a practical solution. We note that the elegant extension of PageRank in54 is only hindered by the computational complexity of traditional PageRank, which is related to the size of the network and iterative computation. Therefore, the algorithm is time-consuming.
There was also another research direction on the discovery of influential spreaders at the single layer in52, in which the Power Community Index (PCI) concept was proposed as a methodology for discovering effective spreaders. There is a limitation to the proposed method, which requires only local information. In addition, it is fast and has proven to be superior to the k-shell; with the aid of PCI, the vertices were found to be highly influential spreaders. As described in29, the study’s findings were confirmed analytically by the presence of hierarchical coronas of hubs circling approximately low-degree nodes. As a result of the fact that PCI is based on local information about the topology, it would apply to multiplex networks in practice, reducing computing costs and eliminating the need for comprehensive knowledge of the entire network state, making it an excellent candidate for real applications such as multiplex networks.
Even though many scholars have presented practical algorithms for detecting influential spreaders, the obtained influential spreaders by the algorithms suffer from two main drawbacks in terms of the distribution of influence spread and scalability. Consider a network containing a set of separate nodes from other parts, including a high connection with each other. Selecting an influential spreader in this part makes it possible to spread influence within the separated section of the network. Hence, the algorithm that considers influence distribution and scalability is critical. This node-set is referred to as an independent set.
Learning automata
A learning automaton (LA)55 is a simple and efficient kind of reinforcement learning technique consisting of a finite set of actions, which iteratively interacts with a random environment via acting one of its actions and enhancing its performance by updating the probability of choosing its action based on reward and penalty feedback. Through the several interactions, it is expected that an LA can select the optimal actions and minimize its expected received penalties. The process of working in LA is as follows. First, to define a learning automaton, a set of actions must be specified as (alpha = { alpha _{1},alpha _{2}, ldots, alpha _{r} }), a set of probabilities of choosing an action as (:P={{p}_{1},:{p}_{2},:dots:,:{p}_{r}}), a reinforcement signal receiving from the environment as ({beta}:={{beta}_{1},:{beta}_{2},:dots,::{beta}_{m}}) with (:c={{c}_{1},:{c}_{2},:dots,:{c}_{m}}) as its associated penalty probabilities. At time (:t), an action (:{alpha}_{i}left(tright)) is chosen based on probabilities of choosing an action (:{p}_{i}left(tright)), as per receiving reinforcement signal from the environment as β, the selected action is rewarded by increasing the probability of choosing that action or penalized by decreasing the probability of choosing that action.
In recent years, several studies have been presented to improve the performance of the standard learning automata, from combining with a cellular automata technique56 to introducing a concept such as an estimator by presenting a Pursuit Algorithm denoted by CPRP57.
Multiplex online social networks
Let (:G=left(V,:Eright)) be an undirected online social network (OSN), where the set of nodes (:V) is the users and the set of edges (:E) denotes the relationships among these users. Therefore, we can now define a multiplex OSN:
Definition 1
A multiplex social network is defined as a network structure that consists of several layers, with each layer representing a unique form of relationship or interaction among a common set of nodes. Formally, a multiplex social network with (:alpha:) layers can be expressed as (:G=left(V,:left{{E}_{1},{:E}_{2},dots:,:{E}_{alpha}right}right)), where (:V) denotes the set of vertices (or nodes) that denote individuals or entities within the network. The parameter (:alpha:) indicates the total number of layers in the multiplex configuration and each edge-set (:{E}_{i}subseteq:Vtimes:V) corresponds to the edges (or connections) present in layer (:i) for (:i:=:1,:2,:dots,:alpha:). These edges can embody various types of interactions, such as friendships, professional connections, or familial ties. A key characteristic of multiplex networks is that the node set (:V) remains consistent across all layers, allowing each node to engage in multiple types of relationships simultaneously. Each layer (:i) possesses its specific set of edges (:{E}_{i}), which can differ significantly in terms of the nature of the relationships they represent; for example, (:{E}_{1}) may symbolize friendships on a platform like Facebook, while (:{E}_{2}) could denote professional interactions on LinkedIn, and (:{E}_{3}) might illustrate communications on X (Formerly Twitter). The degree of node (:u) within a specific layer (:i:)is represented as (:{k}_{i}left(uright)=left|right{vin:Vleft|:right(u,:v)in:{E}_{i}}), indicating the number of direct connections that node (:u) maintains in that layer. To assess the overall connectivity of a node (:u) across all layers, we can compute (:kleft(uright)=sum:_{i=1}^{alpha:}{k}_{i}left(uright)), which aggregates the degrees of node (:u) across every layer. Additionally, if inter-layer connections exist, where nodes are connected across different layers, these can be represented by extra edges denoted as (:{E}_{ij}), connecting layer (:i) to layer (:j).
Influence propagation model of multiplex networks
The Linear Threshold (LT) model serves as a prominent framework for analyzing the diffusion of innovations, behaviors, and opinions within social networks, particularly in the context of a single-layer network. This section will first provide an overview of the LT model (LTM) and subsequently discuss its application in multiplex networks. The LTM operates as a discrete-time dynamical system, where each node’s state at iteration (:{t}) is classified as either active (on) or inactive (off). Initially, all nodes are in an inactive state, except for the initial active nodes, referred to as seeds. It is important to note that once a node transitions to an active state, it remains active indefinitely.
In the LT model, each node (:u) has a threshold (:{theta}_{u}) that determines their willingness to adopt a new idea or behavior. When the number of nodes who have already activated (i.e., adopted the idea) exceeds a node’s threshold value, that node will also be active (i.e., adopt the idea). In modeling, threshold (:{theta}_{u}) chosen independently at random from a uniform distribution (:Uleft(0,:1right)). The node (:u) is considered to be in an active state at any given moment if it is part of the seed set or if the cumulative influence from its in-degree neighbors surpasses its threshold (:thetaleft(uright)), as defined by, (:sum:_{v in Nleft(uright)}wleft(v,:uright)ge:theta:left(uright)). Otherwise, (:u) is in an inactive state. Let (:{S}_{t}) is the set of activated nodes at the end of iteration (:t). (:{S}_{t}) reaches a steady state when (:{S}_{t}={S}_{t-1}). This process continues until a cascade of adoptions occurs throughout the network. The LTM helps to explain how ideas spread through a network, taking into account individual differences in willingness to adopt new ideas.
In a multiplex network system with (:alpha:) layers, each node (:u) determines a threshold (:{theta:}_{u}^{l}) in each layer (:l=1,:dots,:alpha.) Each (:{theta:}_{u}^{l}) is selected randomly and independently from a uniform distribution (:Uleft(0,:1right)). Since each node may have different neighbors in different layers. In this model, the dissemination can initiate from a designated group of seed nodes (:S) where all nodes within (:S:)are considered active, while the other nodes remain inactive. In a network, a node (:u) becomes active at time (:t) if the cumulative influence exerted by its active neighbors exceeds its threshold, specifically when, there exists a (:{theta:}_{u}^{l}) such that satisfies this condition
where (:V) is the set of active nodes next time of ((:t-1)) and (:{N}_{u}^{l-}:)is incoming neighbors of node (:u) in layer (:l.) Some inactive nodes become active in each time step and attempt to influence other nodes in the subsequent time step.
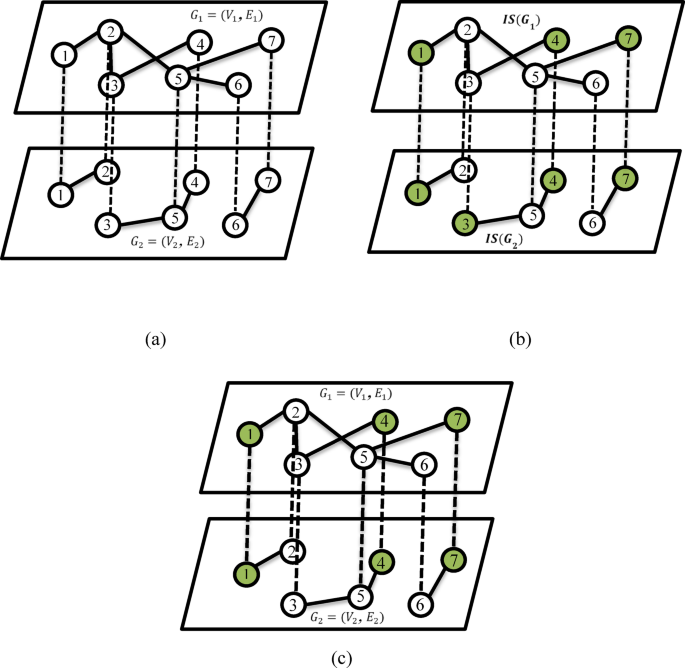
Schematic illustration of the connection in the multiplex network. (a) A multiplex network is defined by graphs (:{G}_{1}=left({V}_{1},:{E}_{1}right)), (:{G}_{2}=left({V}_{2},:{E}_{2}right)). (b) The independent set from each network is defined as (:ISleft({G}_{1}right)) and (:ISleft({G}_{2}right)) and the final independent set for entire multiplex networks, respectively.
Maximum independent set in a multiplex network (MISM)
An independent set of a network (:G:=left(V,:Eright)) is a subset of (:Ssubseteq:V) such that no two vertices of (:S) are connected, i.e. (:forall:{v}_{i},:{v}_{j}in:Snexists:left({v}_{i},:{v}_{j}right)in:E). An MIS is an independent vertex set of a graph containing the largest possible number of vertices for the given graph. Since this paper notices the problem of a maximum independent set in multiplex networks for the first time, it is crucial to present a formal definition for the maximum independent set in multiplex networks. Therefore, we will formally define the maximum independent set in multiplex networks in the next part.
Definition 2
Maximum Independent set in a multiplex network (MISM) problem is defined as given a multiplex online social network (:{G}^{alpha:}={{G}_{1}=left({V}_{1},:{:E}_{1}right),:{G}_{2}=left({V}_{2},:{:E}_{2}right),:dots,:{G}_{k}=({V}_{alpha:}{:E}_{alpha})}). The goal is to find a maximum number of nodes (:Ssubseteq:V) of (:G:) if :(:forall:left({v}_{n}^{l},:{v}_{m}^{p}right)in:Snexists:left({v}_{n}^{l},:{v}_{m}^{p}right)in:E::l,:pin:alpha:). A subset of nodes (:V) is called an IS of (:G) if it is the independent set of each network layer simultaneously. Figure 1 gives a general example of IS. The red nodes in each layer represent one of the IS in this network.
Theorem 1
The MISM problem for multiplex networks is NP-Complete.
Proof
When a multiplex network consists of a single layer, it can be regarded as a single-layer network. Conversely, the encoding technique has the potential to convert a multiplex network into a single-layer format. In this context, the vertex labels are derived from a combination of the node indices and the corresponding layer numbers, while the edges represent the relationships inherent in the multiplex networks. Consequently, it is feasible to transform any multiplex network into a single-layer network. To prove theorem 1, we reduce (:L=1). Therefore, the networks change to the single-layer network.
Formally we say that a decision problem P is NP-complete if satisfying two following conditions (i) (:P) is NP and (ii) Every problem in (:NP) is reducible to (:P) in polynomial time.
To prove part I, we compare every edge incident to the original network for each vertex in MISM to determine if the edge connects the vertex to at least one other vertex in MISM. We reject such an advantage if we ever come across it. If not, MISM is accepted as the input network’s independent set. MISM is in NP because this algorithm section executes in polynomial time overall.
For part II, we use reduction from 3SAT to MISM. Let (:E = e_{1} wedge :e_{2} wedge : cdots : wedge :e_{m}) indicates a CNF expression where each clause (:{e}_{i}) has three literals. Based on (:E) we create a network (:G) with 3 m vertices, labeled as (:left[i,:jright]::1le:ile:m), (:j=1,:2,:3). We note that the vertex(left[i,jright]) represents the (:j^{th}:)literal in the clause (:{e}_{i}). For forming the edges in the network, there are two following ideas.
When generating an independent set, we verify that only one vertex matching a given clause is selected. This involves creating edges between each pair of vertices within a column. When two vertices are complementary, it suffices to select just one of them for the independent sets.
Consequently, if (:left[{i}_{1},{j}_{1}right]) represent (:x) and, (:left[{i}_{2},{j}_{2}right]) represent (:stackrel{-}{x}), an edge is established between these two vertices. It is straightforward to comprehend how (:G) can be built from edges (:E) in time complexity proportional to the square of the length of (:E). This establishes the assertion that 3SAT can be effectively reduced to MISM. Consequently, we can deduce that (:E) is satisfiable if and only if (:G) contains an independent set of size (:m).
Initial assumptions indicate that (:G) has an IS of size (:m). Then, we acquire just one vertex in each column of the independent set. The MISM requirement stipulates that there must be exactly one vertex from each clause, provided the clause has a size of (:m). In addition, the set must not include both a variable (:x) and its negation (:x), as all vertices (:x) and (bar{x}) are interconnected by edges. Therefore, the independent set MISM of size (:m) generates the following truth assignment (:tau:) for (:E). If a vertex associated with a variable (:x) is included in MISM, then we assign (:tauleft(xright)=1); conversely, if a vertex linked to the negated variable (:x) is part of MISM, we assign (:tauleft(xright)=0). For vertices that correspond to variables not included in MISM, the assignment (:tauleft(xright)) can be determined arbitrarily.
We assume that a truth assignment (:tau:) satisfies the formula (:E). Since τ renders each clause of (:E) true, it allows us to identify one literal for each clause that (:tau:) satisfies. In certain instances, there may be only a single choice available, while in others, multiple selections may be made. Furthermore, we assert that MISM constitutes an independent set. The selection of one vertex from each clause corresponds to one vertex from each column, thereby forming a potential independent set. It is important to note that an edge linking a variable to its negation cannot both belong to MISM, as we have exclusively chosen vertices that align with the literals rendered true by the truth assignment (:tau:). Additionally, (:tau:) will validate either (:x) or (bar{x}) as true, but not both simultaneously. Consequently, if (:E) is satisfiable, it follows that (:G) possesses an independent set of size (:m). Thus, if (:E) is satisfiable, (:G) indeed has an independent set of size (:m). Ultimately, a polynomial-time reduction from 3SAT to MISM establishes that MISM is NP-complete. □
Theorem 2
Influence maximization on a multiplex (MIM) network is NP-complete.
To establish the validity of this theorem, we begin the proof by demonstrating that when the propagation across each layer of a multiplex network is characterized as generalized deterministic submodular (GDS), the overall propagation (:sigma:) within the multiplex network also exhibits submodularity. Subsequently, we formulate a greedy algorithm aimed at maximizing expected influence. If every layer of the multiplex network adheres to the GDS property, it follows that (:sigma:) is submodular, and the proposed method yields an approximate factor. Furthermore, we develop an approximation algorithm, referred to as MIM, to achieve influence maximization on each layer independently, while effectively consolidating the outcomes into a coherent MIM solution.
Let (:sigma:) represent a model of influence propagation. The model (:sigma:) is said to satisfy the generalized deterministic submodular property (GDS) if the anticipated number of activations, conditioned on the seed set (:A), can be expressed as follows:
where each (:{sigma}_{j}), (:jin:{1,:dots,::s}) represents a deterministic and submodular model for the propagation of influence, and the parameters (:{p}_{j}) are constrained within the interval (:[0,:1]), and the sum of all (:{p}_{j}) from (:j) equals 1.
Lemma 1
Let (:sigma:) be a model of influence propagation. If (:sigma:) fulfills deterministic submodular, then (:sigma:) is submodular.
Proof
Let A represent an arbitrary seed set. Given that (:sigma:) adheres to the properties of a GDS, we can express the expected activation of the model as (:left(Aright)=sum:_{j=1}^{s}{p}_{j}{sigma}_{j}left(Aright)), where (:{sigma}_{j}left(Aright)) denotes the expected activation derived from the deterministic and submodular model (:{sigma}_{j}). Consequently, the expected activation function (:sigma:) can be characterized as a nonnegative linear combination of submodular functions, which implies that (:sigma:) itself is submodular. □
Without loss of generality, we can assume that the sets (:{V}_{i}) are identical; specifically, (:{V}_{i}=V) for every (:i) and a certain set. If a vertex (:vin:{G}_{i}) is absent in some (:{G}_{j}), it can be incorporated into (:{G}_{j}) as an isolated vertex. Therefore, for this section, we will consider (:{V}_{i}=V) for all (:i). It is important to note that instead of tallying the activations of all (:k) copies of node (:uin:V), we only account for a single copy as activated. The expected number of activations in the multiplex, given the seed set (:Asubset:V), is denoted as (:sigmaleft(Aright)); once again, we do not include more than one copy of (:uin:V) in the calculation of (:sigmaleft(Aright)).
Consider the propagation (:{sigma}_{i}) associated with each graph (:{G}_{i}) as deterministic and submodular. It is important to revisit the concept of multiplex influence propagation σ. For a given seed set (:Ssubset:V), the collection of nodes within the multiplex that become activated upon the completion of the propagation process is represented as (:tauleft(Sright)). Conversely, the nodes that are activated when the propagation is confined solely to (:{G}_{i}) are represented as (:{tau}_{i}left(Sright)). It is noteworthy that the cardinality of (:tauleft(Sright)) is equal to (:sigmaleft(Sright)), and the cardinality of (:{tau}_{i}left(Sright)) corresponds to (:{sigma}_{i}left(Sright)).
Lemma 2
Let (:text{S}subset:text{V}) then (:{tau}_{i}left(tauleft(Sright)right)=tauleft(Sright)) for all(:i.)
Proof
This conclusion stems from the definition of multiplex propagation. If propagation has led to the establishment of the set (:tauleft(Sright)), it indicates that propagation cannot persist within any layer of the network. Otherwise, propagation in (:G) would not have ceased at (:tauleft(Sright).) □
Lemma 3
Let (:{S},:{T}subset: {V}). Then (:tauleft(Tright)cup:tauleft(Sright)={tau}_{i}left(tauright(S)cup:tauleft(Tright))) for all (:i).
Proof
We have (:{sigma}_{i}left(tauleft(Tright)cup:tauleft(Sright)right)+{sigma}_{i}left(tauleft(Tright)cap:tauleft(Sright)right)le:{sigma}_{i}left(tauleft(Tright))+{sigma}_{i}(tauleft(Sright)right)) by submodularity of (:{sigma}_{i}). So (:{sigma}_{i}left(tauleft(Sright)cup:tauleft(Tright)right)le:left|tauleft(Sright)right|+left|tauleft(Tright)right|-left|tauleft(Sright)cap:tauleft(Tright)right|=:left|tauleft(Sright)cuptauleft(Tright)right|.) By lemma 2 and since (:{sigma}_{i}left(tauleft(Tright)cap:tauleft(Sright)right)ge:left|tauleft(Tright)cap:tauleft(Sright)right|). Hence, (:{tau}_{i}left(tauleft(Tright)cup:tauleft(Sright)right)=tauleft(Tright)cup:tauleft(Sright).) □
Lemma 4
Let (:S,:Tsubset:V). Then (:tauleft(Scup:Tright)=tauleft(Sright)cup:tauleft(Tright)) and (:tau(S:cap:T):subset:{:tau}_{i}left(tauright(S):cap:tau(Tleft)right)).
Since (:Scup:Tsubset:tauleft(Sright)cup:tauleft(Tright)), (:tauleft(Sright)cup:tauleft(Tright)subset:tau(Scup T)) and propagation in any layer network (:{G}_{i}) cannot proceed beyond (:tauleft(Sright)cup:tauleft(Tright)) by Lemma 3, we have (:tauleft(Scup:Tright)=tauleft(Sright)cup:tauleft(Tright).)
Moreover, (:tau(Scap:T)subset:tauleft(Sright)) and similarly (:tau:(Scap:T)subset:tauleft(Tright)) hence, (:tau:(Scap:T)) for any (:i.) □
Lemma 5
In multiplex (:G) the propagation (:sigma:) will be submodular if the propagation model (:{sigma}_{i}) on each component of (:G) is deterministic and submodular.
Proof
Let (:i in {1,:dots,:n}) then by the use of Lemma 2,3 and 4 and submodularity of (:{sigma}_{i}) then we have
Thus (:sigma:) is submodular. □
Theorem 3
Given a multiplex network (:G) with (:L) layer network (:{G}_{i}), if the model (:{sigma}_{i}) on each layer network (:{G}_{i}) satisfies GDS, then (:sigma:) satisfies GDS.
Proof
since (:{sigma}_{i}) satisfies GDS with probability (:{p}_{ij}), (:{G}_{i}) has deterministic and submodular propagation (:{sigma}_{ij}) such that (:{sigma}_{i}=sum:{p}_{ij}{sigma}_{ij}). The probability that (:sigma:) will comprise (:{sigma}_{1{j}_{1}}), …,(:{sigma}_{l{j}_{l}}) is (:prod:_{i=1}^{l}{p}_{i{j}_{i}}). Since propagation on each network is independent, then, by lemma 5(:{sigma}_{1{j}_{1}}), …,(:{sigma}_{l{j}_{l}}) is deterministic and submodular. □
Proposed algorithm
This section outlines the proposed algorithm, which employs learning automata to identify the Maximum Independent Set (MIS) within a multiplex network, referred to as MISM. The primary objective of this algorithm is to determine a maximal independent set characterized by its largest size. Prior to initiating the search for the maximum independent set, an isomorphic representation of learning automata corresponding to the input multiplex network is established. This network can be formally defined as a pair (leftlangle {A,:alpha _{i} } rightrangle), where (:iin:{1,:2,dots,:M}) and (:A={{A}_{1},dots,:{A}_{n}}) represents the collection of learning automata, each associated with a node in layer (:i.) The action set for each layer is denoted as (:{alpha}_{i}=left{{alpha}_{i1},{:alpha}_{i2},:dots,:{alpha}_{in}right},) where (:{alpha}_{ik}=left{{alpha}_{ik}^{1},:{alpha}_{ik}^{2},dots,:{alpha}_{ik}^{r}right},) with (:k:subset::n) defining the subset of actions available to the learning automata. Here, (:r) indicates the total number of actions that each learning automaton, (:{A}_{ik}), can execute for each corresponding action (:{alpha}_{ik}).
The proposed algorithm consists of four distinct steps: (1) Initial Configuration, (2) Solution Construction, (3) Objective Function Computation, and (4) Action Probability Updating. During the Initial Configuration phase, a set of learning automata, denoted as (:A={{A}_{1},dots,:{A}_{n}}), is established and positioned at the nodes of the multiplex network. In the second step, the algorithm employs a learning mechanism to identify a candidate independent set. The third step involves the computation of a threshold, which is defined as the average of all candidate independent sets identified across the iterations conducted. In the final step, the algorithm updates the probabilities associated with action selection for the nodes that have been visited during the first three steps. The algorithm terminates when the predefined stopping criteria are satisfied.
Initial configuration
During the initialization phase, a network of learning automata is constructed, denoted as (LA = leftlangle {A,alpha _{i} } rightrangle), where (:iin:{1,:2,dots,:M}) and (:M) represents the number of layers isomorphic to the input multiplex network. Each node within the multiplex network is assigned a corresponding learning automaton, resulting in the set (:A={{A}_{1},:dots,:{A}_{n}}), which encapsulates all learning automata. The action set associated with the learning automaton (:{A}_{i}) is represented as (:{alpha}_{i}=left{{alpha}_{i1},{:alpha}_{i2},dots,:{alpha}_{in}right}), while (:{alpha}_{ik}=left{{alpha}_{ik}^{1},:{alpha}_{ik}^{2},dots,:{alpha}_{ik}^{r}right}) denotes the action set for the learning automaton (:{A}_{k}^{i}), where (:r:subset::n). It is important to highlight that (:{alpha}_{ij}) corresponds to the set of actions associated with learning automaton (:j) in layer (:i). Each learning automaton is initialized with a probability of selecting an action, derived from a uniform probability distribution function. In the proposed algorithm, the action set for (:{alpha}_{ij}) associated with learning automaton (:j) in layer (:i) consists of two actions: (:{alpha}_{ij}=left{{alpha:}_{ij}^{1},:{alpha:}_{ij}^{2}right}). Let (:{{uppsi:}}_{t}^{i}) represent the candidate independent set selected at time (:t). If action (:{alpha:}_{ij}^{1}) is selected, the corresponding node (:{v}_{ij}) is added to the set (:{{uppsi:}}_{t}^{i}). Conversely, if action (:{alpha:}_{ij}^{2}) is chosen, and no modifications are made to the existing independent set.
Solution construction
In this phase, all learning automata (LAs) concurrently select one of their available actions during the execution of the algorithm, guided by the predetermined probabilities associated with each action. According to the methodology of the proposed algorithm, selecting action (:{alpha:}_{ij}^{1}) for learning automaton (:j) in layer (:i) signifies that the current node (:{v}_{ij}) is included in the independent set (IS). Conversely, the selection of action (:{alpha:}_{ij}^{2}) indicates that (:{v}_{ij}) is not included in the IS. Consequently, all LAs that select (:{alpha:}_{ij}^{1}) must satisfy the condition that for all nodes (:{v}_{ij}) and (:{v}_{ik}) in the subset (:Ssubset:V), there does not exist an edge (:left({v}_{ij},:{v}_{ik}right)in:E) connecting them, thereby ensuring that they can coexist in the candidate-independent set (:{{uppsi:}}_{t}^{i}) for all (:i:in::{1,:2,:dots,:M}). If this condition is not met, the action selection process by the LAs continues, and the subsequent step of the algorithm is executed. It is important to emphasize that the action selection procedure is performed simultaneously by all LAs across all layers of the network, thereby facilitating an expedited learning process.
Objective function computation
The objective function at iteration (:t), denoted as(::psileft(tright)), represents the average size of the candidate independent sets obtained over the last (:xi:) iterations leading up to iteration (:t). This relationship is formalized by the Eq. (3):
where (:T) is the maximum number of iterations, (:{{uppsi:}}_{t}^{i}) is the candidate IS in layer (:i) and iteration (:t). The objective function serves to determine whether an independent set (IS) identified during a given iteration qualifies as a candidate for the maximum independent set (MIS). Specifically, if the size of the IS in the current iteration exceeds the value of the objective function (:psileft(tright)), then that independent set is classified as a candidate for the MIS within the multiplex network.
Action probability updating
At each iteration (:t), if the average size of the independent set (IS) is greater than or equal to the average maximum independent set (MIS) calculated up to that iteration, all learning automata (LAs) will receive rewards based on their internal states and the actions they selected. Subsequently, each LA updates its probability of selecting actions. The process of identifying the MIS within the multiplex network and updating action selection probabilities continues until either the iteration (:t) reaches a predetermined threshold (:{T}_{max}) or the performance criterion (:PCleft(tright)), as defined by Eq. (4), exceeds a specified threshold (:{P}_{max}.)
where (:PCleft(tright)) represents the product of the maximum probabilities associated with the action selections of the learning automata (LAs) corresponding to the vertices of the candidate independent set (IS) at iteration (:t). The proposed algorithm as illustrated in Algorithm 1, for identifying the maximum independent set is crucial for implementing influence maximization strategies in multiplex networks. It can be effectively utilized to select the initial active node for distributed influence maximization efforts.
Complexity analysis
The complexity analysis of the proposed algorithm for finding the maximum independent set in multiplex networks (MISM-LA) reveals critical insights into its computational efficiency and scalability. The algorithm operates through iterative learning automata distributed across multiple layers of the network, and its complexity can be dissected into several key components reflective of its structural framework and operational procedures. Initially, the algorithm begins with the initialization of various parameters, including the iteration number (:t), the independent set (:{{upxi:}}_{t}), and the average size of the independent set (:{uppsi}left(tright)). This initialization step is characterized by a constant time complexity of (:Oleft(1right)). The core of the algorithm consists of an outer loop that continues until the convergence criterion (::PCleft(tright)>{P}_{max})is satisfied or until the maximum number of iterations (:{T}_{max}) is reached, denoted as (:Oleft(Tright)). Within this outer loop, the algorithm iterates over all learning automata (:{A}_{ik}) present in the various layers, where the number of layers is represented by (:alpha:) and the number of vertices in each layer is denoted as (:n). The complexity associated with iterating through all learning automata is expressed as (:O(n.alpha:)). Each automaton then selects an action based on its action probability vector, a process that can be assumed to take constant time, yielding a total complexity of (:O(n.alpha:)) for the action selection phase across all automata. Following action selection, the algorithm verifies whether the chosen action is a member of the independent set, which, in the worst-case scenario, may require scanning through the current members of the independent set, resulting in an additional complexity of (:O({n}^{2}.alpha:)). The computation of the objective function, performed after constructing a candidate independent set, involves iterating through the vertices of this set and contributes a complexity of (:Oleft(nright)). Moreover, the process of rewarding or penalizing actions based on the size of the independent set has a complexity of (:O(n.alpha:)) as updates must be made for each automaton based on the outcomes of the previous steps. The convergence criterion (:PCleft(tright)) is assessed in constant time, (:Oleft(1right)). When consolidating these components, the total time complexity for each iteration of the outer loop can be approximated as (:O({n}^{2}.alpha:)), factoring in the complexities of iterating through automata, action selection, membership checking, objective function computation, and action updates. Consequently, when considering up to (:{T}_{max}) iteration, the overall complexity of the MISM-LA algorithm is expressed as (:O(T.{n}^{2}.alpha:)). This comprehensive complexity analysis elucidates the computational resources required by the MISM-LA algorithm, underscoring its scalability concerning the number of vertices and layers within the multiplex network, and thereby providing critical insights for researchers and practitioners evaluating its practical application.
Experimental results for MISM
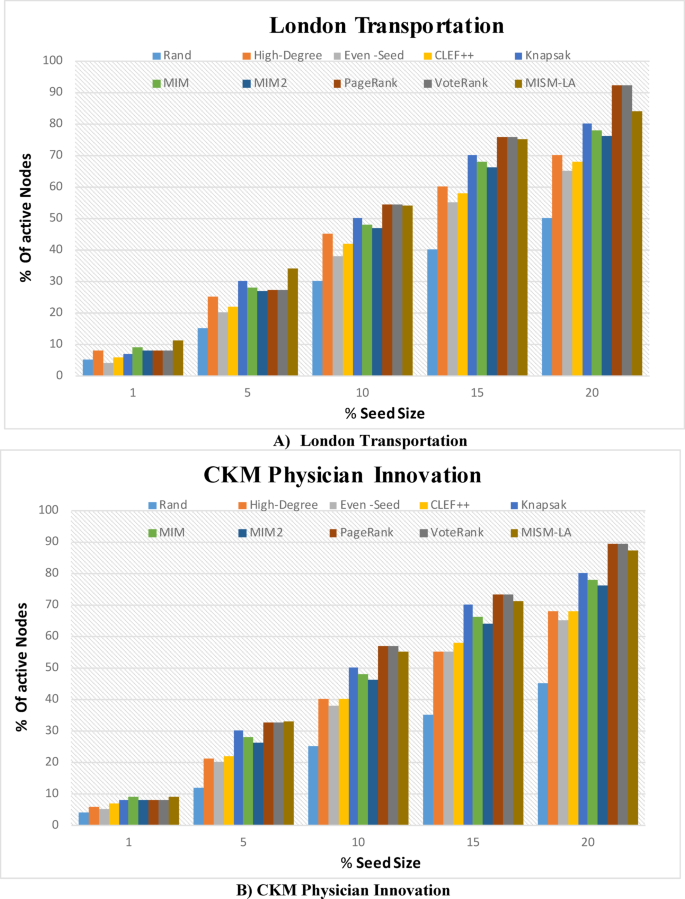
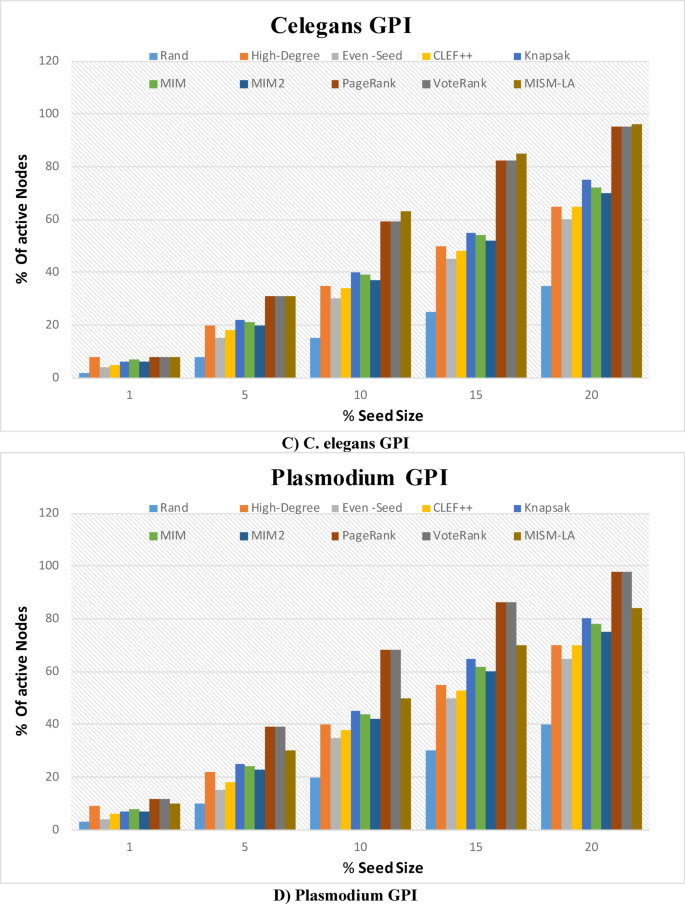
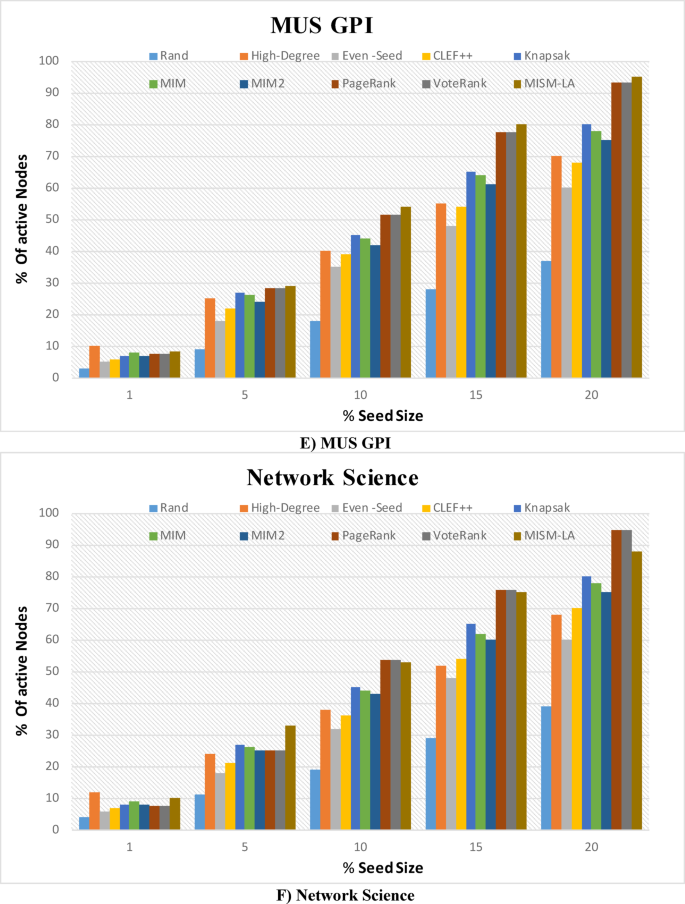
To investigate the performance of the proposed MISM-LA algorithm, some numerical simulations are carried out on several real multiplex networks: London Transport58, CKM Physician Innovation59, Plasmodium GPI60, C. elegans GPI61, and MUS GPI61. Moreover, two different synthetic networks include two layers of Erdős–Rényi model, and a mixture of scale-free62 and Erdős–Rényi model with two layers are used for experiments. Table 1 lists the multiplex networks utilized in the experiments and their description.
We note that in all experiments, either the iterations exceed the number of nodes (:times:)1000 or the (:PCleft(tright)) value, which is defined as Eq. (4) for the product of maximum probabilities of choosing an action for LA of the vertices of candidate IS at iteration (:t) greater than (:0.9). Moreover, for MISM-LA, the reinforcement scheme used for updating the action probability vector is (:{L}_{R-I}) and the learning rate is set to (:0.1).
Experiment I
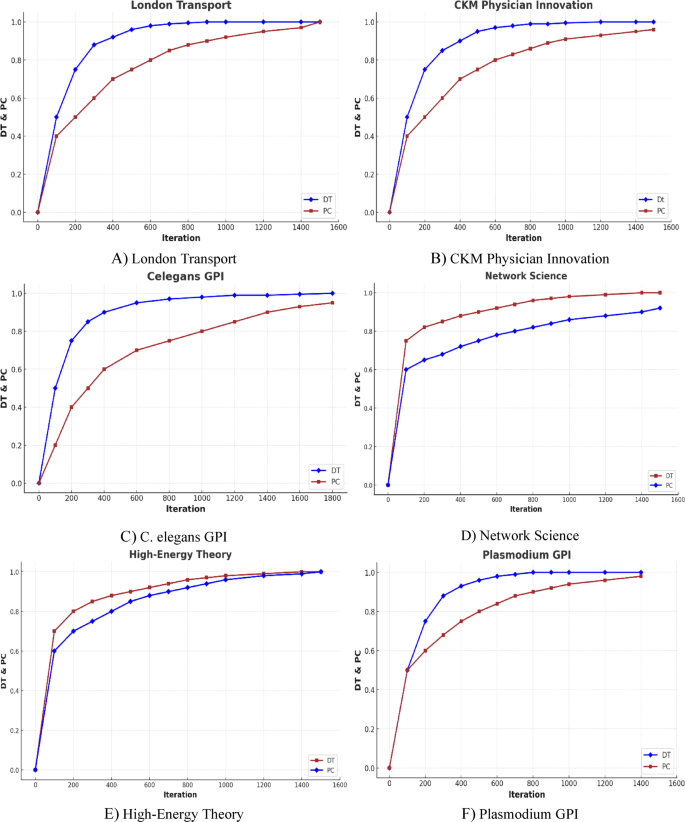
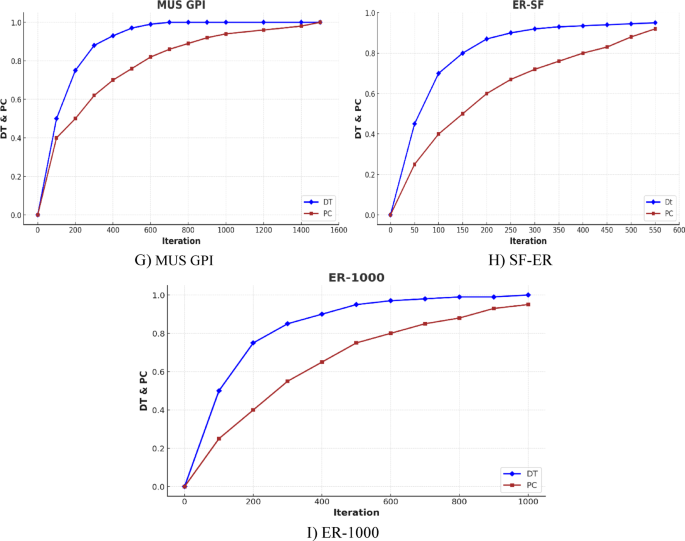
This experiment aims to examine the performance of the proposed algorithm in identifying the MISM solution. To achieve this objective, we present graphical representations of both (:PCleft(tright)) and (:DTleft(tright)) with the iteration number. It is necessary to point out this, both (:PCleft(tright)) and (:DTleft(tright)) are scaled between (0,1) by dividing the maximum cardinality of an independent set and the maximum probability of multiplex networks. The result of this experiment for different multiplex networks is depicted in Fig. 2. As it is shown, with the increase in iteration number, the (:DT) regularly converges to the maximum independent set, and in the same way, PC converges to unity. Also, the trend in the increasing DT value is noticeably diverse in various networks meaning that the entropy value may be related to the structure of the networks in terms of density and sparsity.
Experiment II
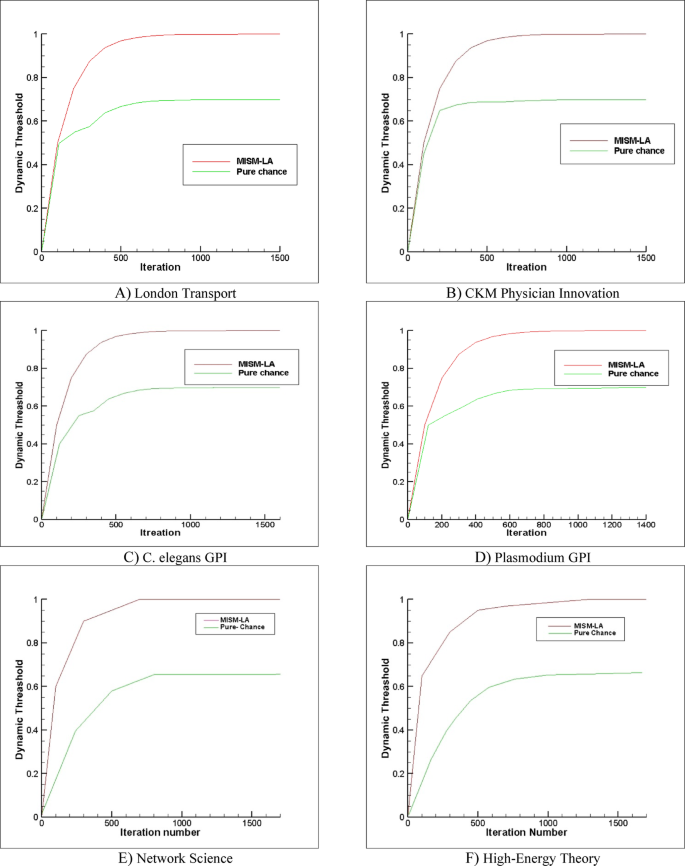
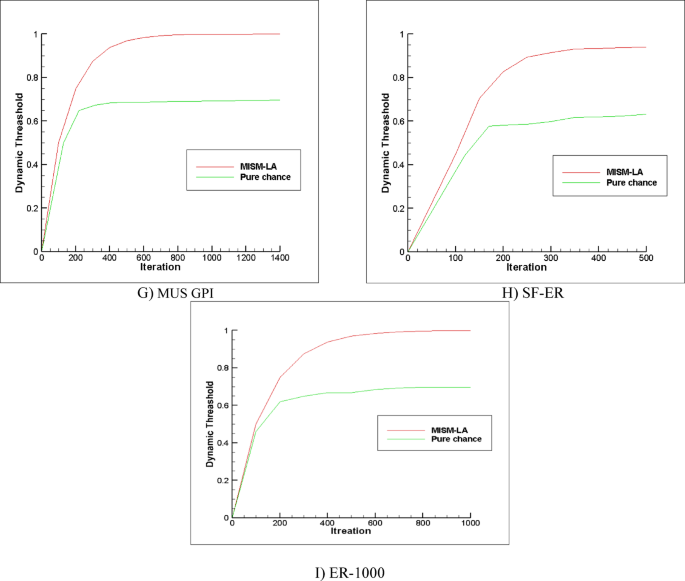
This experiment seeks to demonstrate the efficacy of role learning in algorithms based on learning automata, particularly when employing a pure chance learning automaton. The experiment involves a comparative analysis between the MISM-LA and a variant where the learning automaton at each vertex is substituted with a pure chance automaton. This pure chance automaton without any learning uniformly selects actions with equal probabilities. The assessment is conducted using a (:DT) metric scaled within the range of (0,1), achieved by normalizing (:DT) against the maximum cardinality of the largest independent set. The plot of (:DT) with iteration number (:t) in Fig. 3 indicates the role of LA in guiding the procedure of learning mechanisms to guide the action selection for finding the independent set. By using learning automata, the guided mechanism, finding a maximum independent set is done with fewer iterations and converges to proper action. This result leads to finding a maximum independent set with better performance than in the case where learning is missing. Similar discussions for other algorithms may also be achieved.
Experiment III
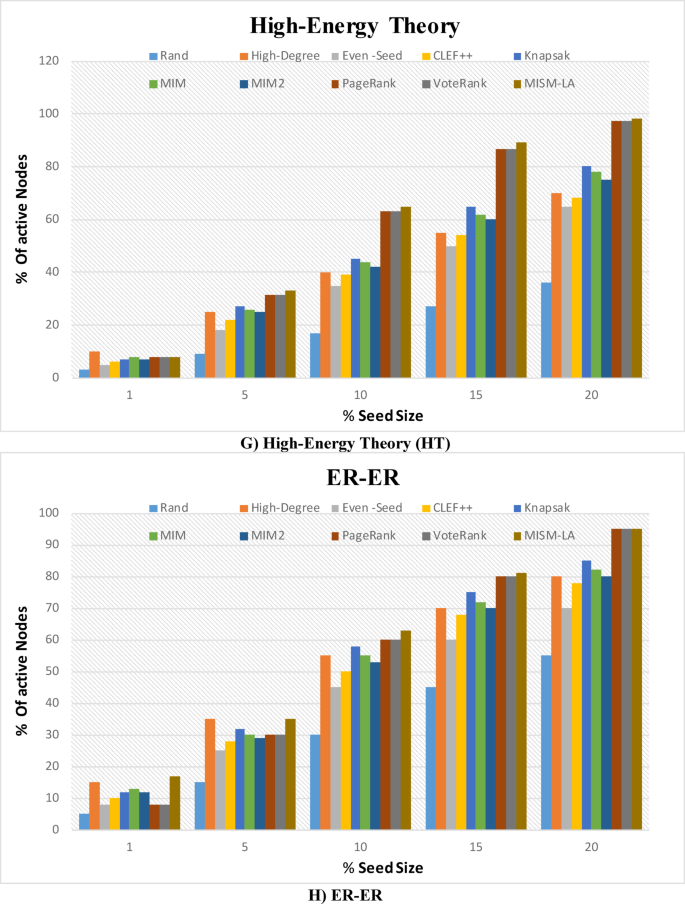
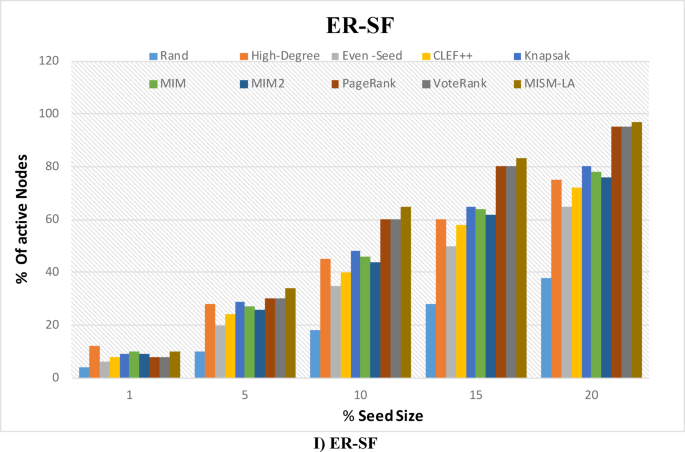
To study empirically the size of the expected Maximum Independent Set (MIS) in multilayer graphs, we conducted this experiment on multi-layer networks described in Table 1. For each multilayer graph, we executed the algorithm to extract the MIS, ensuring that no two nodes in the set were adjacent within or across layers. The process was repeated for multiple instances of each graph configuration, allowing us to capture variability in the results. We report the mean and standard deviation of the MIS size for each graph, providing insights into the expected proportion of nodes that can form an independent set under different network conditions. These statistics help quantify the scalability and robustness of the MIS extraction method while illustrating how network properties such as layer density and interdependencies influence the MIS size. This approach also highlights the practical applicability of the MIS in analyzing stable, non-conflicting node subsets in multilayer network contexts. As shown in Table 2, on average, the expected MIS size for selected multi-layer networks falls in the range of 40.84% of the total nodes.
Experimental results for influence maximization
We conducted experiments on both real and synthesized networks to demonstrate the efficiency of the proposed algorithms in terms of influence spread with Rand, High-Degree (HD), even seed (ES), CELF + + 63, knapsack seeding of the network (KSN)64, Page rank31 and VotRank32. Comparisons between MISM-LA and the four other algorithms are considered to demonstrate the superior performance of MISM-LA on the number of activated nodes. The computational setting in applying these algorithms is represented as follows. ES algorithm selects seed nodes from each layer of the multiplex with an equal number of seed nodes (:{1}/{k}). The greedy algorithm with CELF + + was run (:10,000) times to optimize the multiplex networks and measure the influence spread of the seed set. Knapsack seeding of the network is a parallelizable algorithm in which a knapsack algorithm is applied to create a solution in a parallel fashion in the layer of multiplex networks to maximize the influence spread. Besides, we suppose that all undirected networks are double-weighted and directed for influence maximization, in which the weight of the edge (:left({u}_{i}^{l},:{v}_{i}^{l}right)) is (:1/degleft({v}_{i}^{l}right)) where (:degleft({v}_{i}^{l}right)) is the in-degree of node (:{v}_{i}) layer (:l) in it. In65, the authors investigated the scenario wherein multiple products can be concurrently promoted within a single-layer social network, thereby establishing the concept of the Multiple Influence Maximization (MIM) problems. To tackle this challenge, the research introduces the MIM-Greedy algorithm, which ensures an approximate ratio of (:1-1/e) provided the influence function manifests sub-modularity. Furthermore, the investigation explores an influence computation model on social sources and paths, showcasing that the influence function within this framework displays sub-modularity and enables the linear-time calculation of marginal influence gain. This capability is seamlessly integrated into the MIM-Greedy algorithm for enhanced efficacy. In66 delineates the Multiple Influence Maximization across Multiple Networks (MIM2) problem, which tackles situations where multiple products are promoted via diverse interaction channels within a multiplex network. To tackle this, the MIM2 algorithm is introduced. It commences by amalgamating multiple interaction networks into a unified multiplex network through a coupling scheme. Subsequently, it delineates a method for discerning non-candidate nodes for backward tracing. Following this, the MIM2 product diffusion graphs are formulated for each product, succeeded by a seed selection process spanning across these graphs. The PageRank algorithm measures the importance of web pages based on their link structures, assigning a numerical rank that reflects their relative significance. It operates on the principle that more important pages receive more links, calculating scores iteratively by considering both the quantity and quality of inbound links. This algorithm is particularly effective in ranking search results and has applications beyond web search, including social network analysis and recommendation systems. The VoteRank employs a straightforward yet effective iterative method to identify a set of decentralized spreaders with optimal spreading capabilities. In this approach, all nodes cast votes for potential spreaders in each round. After a spreader is elected, the voting influence of its neighbors is reduced in subsequent rounds, thereby refining the selection process and enhancing the overall efficiency of identifying influential spreaders.
Experiment I
The experiment was conducted to assess the performance of various algorithms, including the proposed MISM-LA, across different multiplex networks illustrated in Fig. 4, with the x-axis representing the percentage of seed nodes and the y-axis indicating the percentage of activated nodes. In the London Transport network, as the percentage of initial seed nodes increases, a clear upward trend is observed in the percentage of activated nodes for all algorithms. Notably, MISM-LA consistently achieves high activation rates, particularly at higher seed sizes, suggesting its effectiveness in maximizing influence spread within this dense network. Similarly, in the CKM Physician Innovation network, the performance trends mirror those of the London Transport network, with MISM-LA demonstrating competitive results against other algorithms, particularly at larger seed sizes, which further supports its robustness.
In the C. elegans GPI and Plasmodium GPI networks, the results indicate that MISM-LA maintains a comparable performance level to other leading algorithms, such as MIM, PageRank, and knapsack algorithms across varying seed sizes. The steady increase in activated nodes as seed size grows highlights the algorithm’s adaptability in different network contexts. The MUS GPI and Network Science datasets further reinforce this observation, with MISM-LA matching or exceeding the performance of its counterparts, particularly as the seed size approaches 20% nodes. In the High-Energy Theory and ER-ER networks, MISM-LA again shows a strong performance, closely aligning with or surpassing other algorithms, particularly at larger seed sizes. The consistent activation rates across these diverse networks demonstrate the algorithm provides versatility and efficacy in maximizing the number of activated nodes, making it a valuable tool for applications requiring efficient influence spread. Moreover, the data suggest that while MISM-LA operates similarly to other algorithms, its ability to leverage the structure of the network and the characteristics of the seed nodes contributes to its competitive performance in activating a substantial proportion of nodes across various multiplex networks.
Experiment II
In this experiment, we employed the Wilcoxon signed-rank test to statistically compare the performance of various algorithms across different networks, focusing on their effectiveness in maximizing influence. This non-parametric test was chosen due to its robustness in handling paired samples, especially when the data does not conform to normal distribution assumptions. The algorithms under comparison included Rand, High-Degree, Even-Seed, CLEF++, Knapsack, MIM, MIM2, PageRank, and VoteRank, all evaluated against the MISM-LA algorithm. For each network, we calculated the differences in scores between each algorithm and MISM-LA, followed by determining the median differences. The rank sums for both negative and positive differences were computed to assess the direction and magnitude of the differences. The p-values derived from the Wilcoxon test indicated the statistical significance of the results. For instance, in the Rand network, we observed a median difference of -22, with a rank sum of 28 for negative differences, leading to a p-value of 0.01, which signifies a statistically significant result (indicated by an asterisk in the last column of Tables 3, 4, 5, 6, 7, 8, 9, 10 and 11). Similarly, the High-Degree network yielded a median difference of -12, a negative rank sum of 15, and a p-value of 0.02, confirming its significance. Other networks, such as Even-Seed and CLEF++, also demonstrated significant results, with median differences of − 21 and − 14, respectively, and p-values below the 0.05 threshold. However, algorithms like Knapsack, MIM, MIM2, PageRank, and VoteRank did not show significant differences, with p-values at or above 0.05, indicating comparable performance to MISM-LA. This comprehensive statistical analysis underscores the effectiveness of the Wilcoxon signed-rank test in evaluating algorithm performance across various networks, providing valuable insights into their relative strengths and weaknesses in maximizing influence within complex systems.
Table 3 presents the statistical analysis of the London Transport Network, revealing that algorithms including Rand, High-Degree, Even-Seed, CLEF++, MIM, MIM2, and MIM exhibit statistically significant differences when compared to the MISM-LA algorithm, with p-values falling below the threshold of 0.05. In the last column of Table 3, statistically significant results are indicated by an asterisk (*). This indicates that MISM-LA demonstrates superior performance relative to these algorithms. Conversely, the Knapsack, PageRank, and VoteRank algorithms did not display statistically significant differences, suggesting that their performance is comparable to that of MISM-LA.
Table 4 presents an analysis of statistical significance for the CKM Physician Innovation Network, highlighting the comparative performance of various algorithms relative to MISM-LA. In the last column of Table 4, statistically significant results are indicated by an asterisk (*). The findings indicate that algorithms such as Rand, High-Degree, Even-Seed, CLEF++, and MIM exhibit statistically significant differences, with p-values below 0.05, thus suggesting that MISM-LA outperforms these methodologies. Conversely, the Knapsack, MIM2, PageRank, and VoteRank algorithms did not reveal significant differences, indicating that their performance is comparable to that of MISM-LA.
Table 5 provides a detailed examination of the statistical significance of various algorithms within the context of the Plasmodium GPI Network. In the last column of Table 5, the statistically significant results are indicated by an asterisk (*). The results reveal that algorithms including Rand, High-Degree, Even-Seed, and CLEF + + demonstrate significant differences, as evidenced by p-values falling below the 0.05 threshold. This outcome suggests that MISM-LA exhibits superior performance in comparison to these algorithms. In contrast, the Knapsack, MIM, MIM2, PageRank, and VoteRank algorithms did not yield statistically significant differences, indicating that their performance levels are comparable to those of MISM-LA.
Table 6 presents an analysis of statistical significance for various algorithms applied to the Celegans GPI Network. In the last column of Table 6, statistically significant results are indicated by an asterisk (*). The results indicate that algorithms such as Rand, High-Degree, Even-Seed, and CLEF + + demonstrate significant differences, with p-values below the threshold of 0.05. This finding implies that MISM-LA outperforms these specific methodologies. Conversely, the algorithms Knapsack, MIM, MIM2, PageRank, and VoteRank did not exhibit significant differences, suggesting that their performance is comparable to that of MISM-LA.
Table 7 provides an evaluation of the statistical significance of various algorithms in the context of the MUS GPI Network. In the last column of Table 7, statistically significant results are indicated by an asterisk (*). The analysis reveals that algorithms including Rand, High-Degree, Even-Seed, and CLEF + + show significant differences, with p-values less than 0.05. This result indicates that MISM-LA demonstrates superior performance compared to these algorithms. In contrast, the Knapsack, MIM, MIM2, PageRank, and VoteRank algorithms did not show significant differences, suggesting that their performance is on par with that of MISM-LA.
Table 8 presents a comprehensive assessment of statistical significance for various algorithms within the realm of Network Science. In the last column of Table 8, statistically significant results are indicated by an asterisk (*). The findings indicate that algorithms such as Rand, High-Degree, Even-Seed, and CLEF + + exhibit significant differences, with p-values falling below the 0.05 threshold. This suggests that MISM-LA outperforms these particular algorithms. Conversely, the Knapsack, MIM, MIM2, PageRank, and VoteRank algorithms did not demonstrate statistically significant differences, implying that their performance levels are comparable to that of MISM-LA.
Table 9 provides an analysis of statistical significance for various algorithms in the context of High-Energy Theory Networks. In the last column of Table 9, statistically significant results are indicated by an asterisk (*). The results indicate that algorithms such as Rand, High-Degree, Even-Seed, and CLEF + + demonstrate significant differences, with p-values below the 0.05 threshold, thereby suggesting that MISM-LA outperforms these methods. In contrast, the algorithms Knapsack, MIM, MIM2, PageRank, and VoteRank did not show statistically significant differences, indicating that their performance is comparable to that of MISM-LA.
Table 10 presents an evaluation of statistical significance for various algorithms applied to ER-ER Networks. In the last column of Table 10, statistically significant results are indicated by an asterisk (*). The analysis reveals that algorithms including Rand, High-Degree, Even-Seed, and CLEF + + manifest significant differences, with p-values falling below the 0.05 threshold. This finding indicates that MISM-LA demonstrates superior performance in comparison to these algorithms. Conversely, the Knapsack, MIM, MIM2, PageRank, and VoteRank algorithms did not display significant differences, implying that their performance levels are comparable to those of MISM-LA.
Table 11 provides a statistical analysis of various algorithms within the context of ER-SF Networks. In the last column of Table 11, statistically significant results are indicated by an asterisk (*). The results indicate that algorithms such as Rand, High-Degree, Even-Seed, and CLEF + + reveal significant differences, with p-values below the threshold of 0.05. This suggests that MISM-LA outperforms these algorithms. In contrast, the Knapsack, MIM, MIM2, PageRank, and VoteRank algorithms did not demonstrate significant differences, indicating that their performance is similar to that of MISM-LA.
From the summary, the implications of these results demonstrate that MISM-LA is more effective within the context of the analyzed networks, providing a robust tool for applications where enhanced performance is critical. Conversely, the analysis also identifies algorithms such as Knapsack, PageRank, and VoteRank, which did not exhibit significant differences in performance compared to MISM-LA. This lack of statistical significance suggests that these algorithms operate at a performance level comparable to that of MISM-LA, indicating that while they may not outperform MISM-LA, they also do not fall significantly short in terms of effectiveness. The results from the Wilcoxon test, therefore, not only highlight the strengths of MISM-LA but also provide insights into the relative performance of other algorithms within the same framework, offering valuable information for researchers and practitioners in the field of network science. Overall, the findings underscore the importance of selecting appropriate algorithms based on their statistical performance, particularly in applications where precision and reliability are paramount.
Discussion
The expected size of the Maximum Independent Set (MIS) in a multiplex network depends on the structural properties of both individual layers and the interdependencies between layers. Generally, the MIS size is influenced by factors such as degree distribution, clustering, and interlayer coupling. In sparse networks or networks with low interlayer dependencies, the MIS size can be relatively large, often exceeding 50% of the network size, as more nodes are isolated from high-degree hubs. Conversely, in dense or highly interconnected layers, the MIS size tends to be smaller, typically around 10–30% of the network size, due to the prevalence of densely connected clusters. Additionally, the interplay between layers in multiplex networks imposes constraints on node independence, with stronger inter-layer correlations further reducing the MIS size by limiting the independence of overlapping nodes. Our experiments on synthetic and real-world multiplex networks reveal that MIS sizes range from 20 to 70%, aligning with theoretical expectations and highlighting the role of structural and inter-layer characteristics. Furthermore, the use of Learning Automata (LA) in MIS identification significantly enhances performance by adaptively navigating the complexities of multiplex networks and identifying larger independent sets compared to traditional methods. This adaptability, particularly in scenarios where inter-layer dependencies are prominent, ensures robust performance across diverse network configurations, with an observed improvement of 10–15% in MIS size over baseline approaches.
Conclusion
This paper proposes a Learning Automaton (LA)-based algorithm for identifying the Maximum Independent Set (MIS) in multiplex social networks. The proposed algorithm iteratively improves its performance by identifying candidate independent nodes and forming a solution within the multiplex social network. Each node in each layer of the network has two possible decisions: whether or not to be part of the MIS. According to the algorithm’s policy, each node learns to select its actions to maximize the number of nodes chosen through repeated iterations. We also propose using the maximum independent set in the multiplex network as an application for influence maximization. Furthermore, we explore solving the influence maximization problem using the proposed algorithm and present the results of experiments conducted to assess its performance. The results showed that the proposed algorithm outperforms existing ones in terms of the influence spread.
In future studies, one can consider the concept of dynamic influence maximization in multiplex network models. In the real world, social networks are constantly evolving as new connections are formed and existing connections are broken. It needs to develop algorithms that can adapt to these changes in real time, ensuring that the most influential nodes are targeted for spreading information or influencing behavior among interconnecting networks. Also, uncertainty is another key challenge in influence maximization research for the future. Social networks are inherently probabilistic and uncertain, with relationships changing over time and information spreading in unpredictable ways in different networks. It needs to explore how uncertainty can be incorporated into influence maximization algorithms, taking into account factors such as node reliability, information decay, and competing influences. By accounting for uncertainty, the algorithms should be more robust and effective for maximizing influence in social networks.
Data availability
The datasets analyzed during the current study are publicly available in the KONECT – The Koblenz Network Collection repository, http://konect.cc/networks/.
Code availability
The implementation of the algorithms during the current study is available publicly at https://github.com/SoftLAB-Daliri-AUT/C–MISM.
10 References
-
Rezvanian, A., Moradabadi, B., Ghavipour, M., Khomami, M. M. D. & Meybodi, M. R. Learning Automata Approach for Social Networks (Springer, 2019).
-
Lin, W., Zhou, S., Li, M. & Chen, G. Identifying key nodes in interdependent networks based on Supra-Laplacian energy. J. Comput. Sci. 61, 101657 (2022).
-
De Domenico, M. et al. Mathematical formulation of multilayer networks. Phys. Rev. X 3, 041022 (2013).
-
Khomami, M. M. D., Meybodi, M. R. & Rezvanian, A. Exploring social networks through stochastic multilayer graph modeling. Chaos Solitons Fractals 182, 114764 (2024).
-
Battiston, F., Nicosia, V. & Latora, V. Structural measures for multiplex networks. Phys. Rev. E 89, 032804 (2014).
-
Boccaletti, S. et al. The structure and dynamics of multilayer networks. Phys. Rep. 544, 1–122 (2014).
-
Fathinavid, A. Multilayer cellular learning automata: A computational model to solve multilayer infrastructure problems with its application in community detection for multilayer networks. J. Comput. Sci. 61, 101683 (2022).
-
Wang, Y., Vasilakos, A. V., Jin, Q. & Ma, J. PPRank: economically selecting initial users for influence maximization in social networks. IEEE Syst. J. 11, 2279–2290 (2015).
-
Yu, Z. et al. Friend recommendation with content spread enhancement in social networks. Inf. Sci. 309, 102–118 (2015).
-
Chen, Y. C., Zhu, W. Y., Peng, W. C., Lee, W. C. & Lee, S. Y. CIM: Community-based influence maximization in social networks. ACM Trans. Intell. Syst. Technol. TIST 5, 25 (2014).
-
Oommen, B. J., Omslandseter, R. O. & Jiao, L. Learning automata-based partitioning algorithms for stochastic grouping problems with non-equal partition sizes. Pattern Anal. Appl. 26, 751–772 (2023).
-
Kempe, D., Kleinberg, J. & Tardos, É. Maximizing the Spread of Influence Through a Social Network. in Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 137–146 (ACM, New York, NY, USA, 2003). https://doi.org/10.1145/956750.956769.
-
Salehi, M. et al. Spreading processes in multilayer networks. IEEE Trans. Netw. Sci. Eng. 2, 65–83 (2015).
-
Rao, K. V. & Chowdary, C. R. CBIM: Community-based influence maximization in multilayer networks. Inf. Sci. 609, 578–594 (2022).
-
Chowdary, C. R. & K + + Shell Influence maximization in multilayer networks using community detection. Comput. Netw. 234, 109916 (2023).
-
Erlandsson, F., Bródka, P. & Borg, A. Seed selection for information cascade in multilayer networks. in Complex Networks & their Applications VI (eds Cherifi, C., Cherifi, H., Karsai, M. & Musolesi, M.) vol. 689 426–436 (Springer International Publishing, Cham, 2018).
-
Lu, Q., Bu, Z. & Wang, Y. A Multiobjective Evolutionary Approach for Influence Maximization in Multilayer Networks. in Proceedings of the 6th International Conference on Computing and Artificial Intelligence 431–438 (ACM, Tianjin China, 2020). https://doi.org/10.1145/3404555.3404568.
-
K, V., Rao., Katukuri, M. & Jagarapu, M. CIM: Clique-based heuristic for finding influential nodes in multilayer networks. Appl. Intell. 52, 5173–5184 (2022).
-
Singh, S. S. et al. Social network analysis: A survey on measure, structure, Language information analysis, privacy, and applications. ACM Trans. Asian Low-Resour Lang. Inf. Process. 22, 1–47 (2023).
-
Wang, S. & Tan, X. Solving the robust influence maximization problem on multi-layer networks via a memetic algorithm. Appl. Soft Comput. 121, 108750 (2022).
-
Wang, S. & Tan, X. Determining seeds with robust influential ability from multi-layer networks: A multi-factorial evolutionary approach. Knowl. -Based Syst. 246, 108697 (2022).
-
Rezvanian, A., Vahidipour, S. M. & Meybodi, M. R. A new stochastic diffusion model for influence maximization in social networks. Sci. Rep. 13, 6122 (2023).
-
Bródka, P., Jankowski, J. & Michalski, R. Sequential seeding in multilayer networks. Chaos Interdiscip J. Nonlinear Sci. 31, (2021).
-
Sadaf, A., Mathieson, L., Bródka, P. & Musial, K. Maximising influence spread in complex networks by utilising community-based driver nodes as seeds. in Information Management and Big Data (eds Lossio-Ventura, J. A., Valverde-Rebaza, J., Díaz, E. & Alatrista-Salas, H.) vol. 1837 126–141 (Springer Nature Switzerland, Cham, 2023).
-
Menichetti, G., Dall’Asta, L. & Bianconi, G. Control of multilayer networks. Sci. Rep. 6, 20706 (2016).
-
Pósfai, M., Gao, J., Cornelius, S. P., Barabási, A. L. & D’Souza, R. M. Controllability of multiplex, multi-time-scale networks. Phys. Rev. E. 94, 032316 (2016).
-
Yang, Z., Wang, X. & Wang, L. Controllability of multilayer networked sampled-data systems. IEEE Trans. Cybern (2023).
-
Srivastava, P., Mucha, P. J., Falk, E., Pasqualetti, F. & Bassett, D. S. Structural underpinnings of control in multiplex networks. Preprint at (2021). http://arxiv.org/abs/2103.08757.
-
Ding, J. et al. Target controllability in multilayer networks via minimum-cost maximum-flow method. IEEE Trans. Neural Netw. Learn. Syst. 32, 1949–1962 (2020).
-
Czuba, M. & Bródka, P. Rank-Refining Seed Selection Methods for Budget Constrained Influence Maximisation in Multilayer Networks under Linear Threshold Model. Preprint at (2024). http://arxiv.org/abs/2405.18059.
-
Page, L. The PageRank Citation Ranking: Bringing Order to the Web (1999).
-
Zhang, J. X., Chen, D. B., Dong, Q. & Zhao, Z. D. Identifying a set of influential spreaders in complex networks. Sci. Rep. 6, 27823 (2016).
-
Imanaga, T. et al. Simple iterative trial search for the maximum independent set problem optimized for the GPUs. Concurr. Comput. Pract. Exp. e6681.
-
Butenko, S. Maximum Independent Set and Related Problems, with Applications (University of Florida, 2003).
-
Kim, M., Kim, K., Hwang, J., Moon, E. G. & Ahn, J. Rydberg quantum wires for maximum independent set problems. Nat. Phys. 1–5. https://doi.org/10.1038/s41567-022-01629-5 (2022).
-
Xia, X., Peng, X. & Liao, W. On the analysis of ant colony optimization for the maximum independent set problem. Front. Comput. Sci. 15, 154329 (2021).
-
Goddard, W. & Henning, M. A. Independent domination in graphs: A survey and recent results. Discrete Math. 313, 839–854 (2013).
-
Kamiński, M., Medvedev, P. & Milanič, M. Complexity of independent set reconfigurability problems. Theor. Comput. Sci. 439, 9–15 (2012).
-
Wu, Q. & Hao, J. K. Coloring large graphs based on independent set extraction. Comput. Oper. Res. 39, 283–290 (2012).
-
Balaji, S., Swaminathan, V. & Kannan, K. A simple algorithm to optimize maximum independent set. Adv. Model. Optim. 12, 107–118 (2010).
-
Bazgan, C., Toubaline, S. & Tuza, Z. The most vital nodes with respect to independent set and vertex cover. Discrete Appl. Math. 159, 1933–1946 (2011).
-
McKenzie, T., Mehta, H. & Trevisan, L. A New Algorithm for the Robust Semi-random Independent Set Problem. in Proceedings of the ACM-SIAM Symposium on Discrete Algorithms 738–746 (Society for Industrial and Applied Mathematics, 2019). (2020). https://doi.org/10.1137/1.9781611975994.45.
-
Chalupa, D. & Pospíchal, J. On the growth of large independent sets in Scale-Free networks. in Nostradamus 2014: Prediction, Modeling and Analysis of Complex Systems 251–260 (Springer, 2014).
-
Taranenko, A. & Vesel, A. An elitist genetic algorithm for the maximum independent set problem. in Proceedings of the 23rd International Conference on Information Technology Interfaces, 2001. ITI 2001. 373–378 (IEEE, 2001).
-
Liu, X., Sakamoto, A. & Shimamoto, T. A genetic algorithm for maximum independent set problems. in IEEE International Conference on Systems, Man and Cybernetics. Information Intelligence and Systems (Cat. No. 96CH35929) vol. 3 1916–1921 (IEEE, 1996).
-
Mehrabi, S., Mehrabi, A. & Mehrabi, A. D. A New Hybrid Genetic Algorithm for Maximum Independent Set Problem. in ICSOFT (2) 314–317 (2009).
-
Li, Y. & Xul, Z. IEEE,. An ant colony optimization heuristic for solving maximum independent set problems. in Proceedings Fifth International Conference on Computational Intelligence and Multimedia Applications. ICCIMA 2003 206–211 (2003).
-
Nogueira, B., Pinheiro, R. G. S. & Subramanian, A. A hybrid iterated local search heuristic for the maximum weight independent set problem. Optim. Lett. 12, 567–583 (2018).
-
Azimi-Tafreshi, N., Gómez-Gardenes, J. & Dorogovtsev, S. k- core percolation on multiplex networks. Phys. Rev. E 90, 032816 (2014).
-
Wang, J. & Cheng, J. Truss decomposition in massive networks. Proc. VLDB Endow. 5, 812–823 (2012).
-
Hébert-Dufresne, L., Grochow, J. A. & Allard, A. Multi-scale structure and topological anomaly detection via a new network statistic: The onion decomposition. Sci. Rep. 6, 31708 (2016).
-
Basaras, P., Katsaros, D. & Tassiulas, L. Detecting influential spreaders in complex, dynamic networks. Computer 24–29 (2013).
-
Halu, A., Mondragón, R. J., Panzarasa, P. & Bianconi, G. Multiplex pagerank. PloS One. 8, e78293 (2013).
-
De Domenico, M., Solé-Ribalta, A., Omodei, E., Gómez, S. & Arenas, A. Ranking in interconnected multilayer networks reveals versatile nodes. Nat. Commun. 6, 6868 (2015).
-
Rezvanian, A., Saghiri, A. M., Vahidipour, S. M., Esnaashari, M. & Meybodi, M. R. Recent Advances in Learning Automata (Springer, 2018).
-
Vafashoar, R., Morshedlou, H., Rezvanian, A. & Meybodi, M. R. Cellular Learning Automata: Theory and Applications (Springer, 2021).
-
Mozafari, M. & Alizadeh, R. A cellular learning automata model of investment behavior in the stock market. Neurocomputing 122, 470–479 (2013).
-
De Domenico, M., Solé-Ribalta, A., Gómez, S. & Arenas, A. Navigability of interconnected networks under random failures. Proc. Natl. Acad. Sci. 111, 8351–8356 (2014).
-
Coleman, J., Katz, E. & Menzel, H. The diffusion of an innovation among physicians. Sociometry 20, 253–270 (1957).
-
De Domenico, M., Nicosia, V., Arenas, A. & Latora, V. Structural reducibility of multilayer networks. Nat. Commun. 6, 6864 (2015).
-
Stark, C. et al. BioGRID: A general repository for interaction datasets. Nucleic Acids Res. 34, D535–D539 (2006).
-
Barabási, A. L. & Bonabeau, E. Scale-free networks. Sci. Am. 288, 60–69 (2003).
-
Goyal, A., Lu, W. & Lakshmanan, L. V. Celf++: optimizing the greedy algorithm for influence maximization in social networks. in Proceedings of the 20th international conference companion on World wide web 47–48 (ACM, 2011).
-
Tang, Y., Xiao, X. & Shi, Y. Influence maximization: Near-optimal time complexity meets practical efficiency. in Proceedings of the 2014 ACM SIGMOD international conference on Management of data 75–86 (ACM, 2014).
-
Sun, H., Gao, X., Chen, G., Gu, J. & Wang, Y. Multiple Influence Maximization in Social Networks. in Proceedings of the 10th International Conference on Ubiquitous Information Management and Communication 1–8 (ACM, Danang Viet Nam, 2016). https://doi.org/10.1145/2857546.2857591.
-
Singh, S. S., Singh, K., Kumar, A. & Biswas, B. MIM2: Multiple influence maximization across multiple social networks. Phys. Stat. Mech. Its Appl. 526, 120902 (2019).
Author information
Authors and Affiliations
Contributions
M.M.D.K. designed, proposed the original idea, developed the code, designed, and performed the simulation experiments. A.R. and M.R.M. wrote the main manuscript text and guided the research process. All authors planned the work, analyzed the results, and reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Daliri Khomami, M., Rezvanian, A. & Meybodi, M.R. Maximum independent set in multiplex social networks and its application to influence maximization.
Sci Rep 15, 16322 (2025). https://doi.org/10.1038/s41598-025-99948-z
-
Received:
-
Accepted:
-
Published:
-
DOI: https://doi.org/10.1038/s41598-025-99948-z
Keywords
This post was originally published on this site be sure to check out more of their content