A topic dissemination model based on hypernetwork

With the rapid advancement of social media and online platforms, studying topic dissemination has become increasingly important, particularly for understanding public opinion, marketing strategies, and information flow in interpersonal networks¹. Many scholars have explored topic dissemination using complex network theory and infectious disease models, formulating various paradigms, such as SIR, SIS, and SIRS^2,3,4. However, these models primarily rely on simple networks, where edges represent only pairwise interactions between nodes. This simplification overlooks multi-way interactions commonly observed in real-world social systems⁵. For instance, on online social media platforms, users not only form pairwise connections through behaviors like following but also participate in group interactions centered around shared interests, topics, or needs. Therefore, traditional graph-based binary simple networks are no longer suitable for such systems. Higher-order network represents an emerging model that extends the traditional network by considering interactions among multiple entities rather than just simple pairwise connections. This extension transforms the dissemination paradigm from one-to-one to one-to-many or even many-to-many interactions⁶.Multi-layer networks⁷, weighted networks⁸ and temporal networks⁹ are important tools for modelling complex networks, and there have been research advances in representing higher-order network data and topology, but they are not intuitive enough to express the higher-order interactions of nodes. Hypernetworks provide a more sophisticated framework where hyperedges connect multiple nodes simultaneously¹⁰, overcoming the limitations of simple networks and enabling scholars to capture the complexity of topic dissemination more comprehensively.

Despite these advancements, existing research on hypernetwork-based dissemination models relies on the assumption of uniformly mixed population, where individuals have the same probability of interacting with others, leading to a uniform spread of infection. This assumption simplifies analysis but neglects real-world heterogeneities such as individual differences in infectiousness and structural complexity of hyperedges^11,12. Individuals also adjust their participation dynamically across various topics based on the number of communicators and activity levels.

Individual characteristics, topic characteristics, and network structure are crucial factors that influence topic dissemination in social networks. Different individuals have unique characteristics in understanding and interpreting information¹³. Those who are highly influential and active can disseminate information more effectively. Topics impact the evolution of macro-level public opinion through characteristics such as information intensity and topic type^14,15. Existing research results on topic propagation (e.g. CSIRS model) help to understand the propagation dynamics of topics, revealing that nodes are sensitive to topic characteristics, and that network structure plays an important role in topic dissemination process, but they have not been applied to hypernetwork structures. Bodó-SIS as one of the earliest hypernetwork propagation models, the constructed hypernetwork model assumes that all hyperedges are internally fully connected and the non-uniform propagation properties of the nodes are not considered in its propagation model, limiting more complex and realistic propagation mechanisms.

In summary, we proposed an improved SIRS dissemination model based on hypernetwork (HSIRS model). The main contributions of this paper are as follows:

1. (1)

   Constructing a hypernetwork structure by enhancing Bodó’s clique-structured hypergraph generation method which can represent users’ interaction more accurately in a given online social network.

2. (2)

   Incorporating user activity levels, information sensitivity, and hyperedge size, thereby addressing the oversimplifications in existing hypernetwork-based models.

3. (3)

   By examining the effects of hyperedge size, topic content, and individual characteristics on topic dissemination, providing theoretical insights for predicting information dissemination and informing public opinion management strategies.

This paper comprises several sections that discuss topic dissemination model based on hypernetwork. Section “Related work” introduces the related work of topic dissemination process in complex networks. Section “Model description” focuses on the proposed hypernetwork generation method and HSIRS model. Section “Simulation and Experimental Analysis ” shows the feasibility and effectiveness of the proposed model. Also, the influences of various factors on topic dissemination are explored.

At the end of the 20th century, the emergence of small-world networks and scale-free networks advanced complex network theory^16,17. Scholars began modeling infectious disease dynamics with networks where individuals are nodes and their interaction relationships are edges¹⁸. Given the similarity between public opinion dissemination and infectious disease dissemination, methods combining complex network theory with epidemiology have become essential in topic dissemination modeling. Current trends in topic dissemination research can be categorized mainly into two areas:

Firstly, traditional topic dissemination models are largely built upon graph-based frameworks, where the classical SIR (Susceptible-Infected-Removed) model serves as a foundational theoretical framework, increasingly applied to topic dissemination across complex systems^19,20,21. Scholars have enhanced the SIR model by introducing additional states or incorporating topic-related factors. For instance, Enatsu et al.²² proposed the SIRS model, accounting for the possibility that immune nodes may revert to susceptible nodes due to certain external factors. Han et al.²³ enhanced the SIRS model for simulating the spread of hot topics in social networks by considering node sensitivity to content and the influence of neighboring nodes on dissemination probability. Zhao Li et al.²⁴ observed that participants vary in popularity and activeness, leading to different dissemination abilities, and they refined the information cascade dissemination model based on node popularity and activeness, providing a more detailed portrayal of each node’s role in the topic dissemination process. However, graph-based models exhibit several inherent limitations in modeling real-world topic dissemination. As noted by Lambiotte. R et al.²⁵, empirical data reveal that the basic pairwise interaction units fail to capture the intricate dependencies inherent in real-world networks.

Secondly, hypergraph-based hypernetworks are studied for modeling complex social connections beyond simple pairwise relationships, given that real-world communication often involves multi-body interactions. The hypergraph is a generalized graph-relational structure that describes relationships between nodes and hyperedges. This representation has broad applications across disciplines such as physics, mathematics, and computer science, where complex relational data must be modeled^26,27,28. Although there have been several research approaches in expressing higher-order networks, but compared to these approaches, hypergraph-based hypernetworks present a more direct representation of group-based propagation in the real world. Multilayer networks represent different types of interactions through different levels of networks and are commonly used for cross-platform research, but are still essentially binary relationships within layers. Weighted networks allow for different weights to be assigned to binary connections to represent different interaction strengths, which approximates some of the higher-order effects but does not allow for the direct modelling of the impact of multibody interactions. Temporal networks are mainly used for portraying the dynamic evolution of the network structure and need to be extended to support the representation of higher-order interactions. Hyperedges can encompass multiple nodes, effectively representing higher-order interactions. Wang et al. presented a heterogeneous hypergraph embedding models for efficient point of interest recommendation systems²⁹. In location-based social networks, neural graph collaborative filtering combined with hypernetwork structures in the study of Acharya et al. has enhanced the accuracy of high-order spatial connection mining³⁰. Furthermore, hypernetworks have been integrated into continual learning frameworks, enabling models to adapt to dynamic environments while retaining historical knowledge³¹. Peng et al. explored cross-platform relational alignment based on multi hypernetwork structure attributes, improving accuracy across different network layers³². Recent studies have demonstrated the distinct advantages of hypernetwork-based models over traditional graph-based models. One of the first attempts to model dissemination on hypergraphs was made by Bodó. In 2016, Bodó³³ introduced a method for generating hyperedges by detecting cliques in power-law random graphs. He proposed the first SIS infectious disease dissemination model on hypergraphs, considering community structure and the nonlinear dependence of infection probability on the number of infected neighbors. However, this method assumed full connectivity between nodes within each hyperedge, which limited its ability to represent dissemination processes in higher-order networks. Bodó-SIS didn’t take into account the dynamic adjustment of the probability of infection of an individual and is therefore less applicable to the evolution of opinion in the real world. Many scholars have explored topic dissemination models on hypernetworks, achieving preliminary progress in some areas. Suo et al.³⁴ analyzed public opinion propagation in hypernetworks, proposing models based on global and local propagation strategies respectively. Hu Feng et al.³⁵ demonstrated the small-world characteristics and information propagation dynamics of hypernetworks by adapting the WS algorithm. Shen Wang et al.³⁶ considered social network topology with both friend and groupmate relationships, incorporating behavioral diversity to enhance the SIR model. These studies employed various methods to construct hypernetwork structures, highlighting that topics in hypernetworks spread faster and reach more audiences. In 2020, Nicholas W et al.³⁷ introduced a hyperdegree-based SIS dissemination model, revealing that hyperedge heterogeneity facilitates discontinuous phase change behavior in infectious disease spread.

Based on existing research, the following considerations are still lacking in current studies focused on topic dissemination modeling on hypernetworks: (1) Most hypernetworks rely on synthetic networks for their construction, and the clique-structured hypernetworks initially proposed by Bodó are limited and identical to simple networks in certain respects. (2) Most current hypernetwork models employ overly simplistic rules for state transitions, neglecting comprehensive consideration of individual activity, topic sensitivity, and hyperedge heterogeneity factors on topic dissemination.

This section will provide a detailed introduction to HSIRS. The hypernetwork is constructed by enhancing Bodó’s clique-structured hypergraph generation method, and the rules for the state transition are formulated based on the hypernetwork by considering the topic characteristics, individual characteristics, and hyperedge size factors.

Hypernetwork construction for online social networks

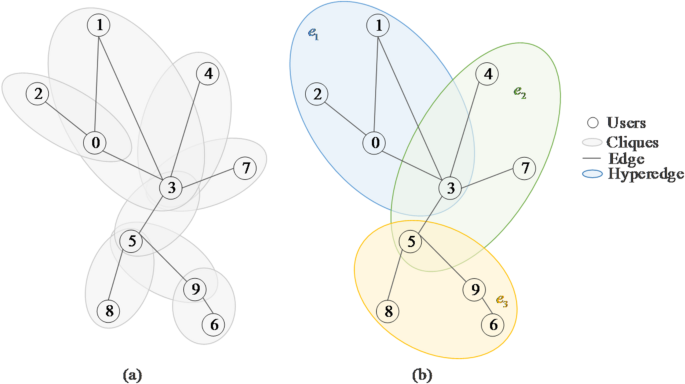
A hypergraph is a generalization of a graph, whereas the network represented by a hypergraph is referred to as a hypernetwork. A hypergraph on a finite vertex set (:V) is denoted as (:H=(V,E)), where (:V={{v}_{1},{v}_{2},dots:,{v}_{n}}) is the vertex set, and (:E={{e}_{1},{e}_{2},dots:,{e}_{m}}) is the set of hyperedges. A hyperedge (:{e}_{i}={{v}_{i1},{v}_{i2},dots:,{v}_{ij}}(i=text{1,2},dots:,m)(1le:jle:n)) is a subset of (:V) that must satisfy (:{e}_{i}ne:{Phi:}(i=text{1,2},dots:,m)) and (:bigcup:_{i=1}^{m}{e}_{i}=text{V}). The hyperdegree of a node (:{v}_{i}) denoted (:{d}_{H}left(iright)) is defined as the number of hyperedges containing that node. The degree of a hyperedge (:{e}_{i}) denoted (:kleft({e}_{i}right)) is defined as the number of vertices contained within the hyperedge and is used to measure hyperedge size. If a node (:{v}_{i}(ile:n)) and a node (:{v}_{j}(jne:i,jle:n)) belong to the same hyperedge, then nodes (:{v}_{i}) and (:{v}_{j}) are considered neighbors.

In this paper, we will extend the method of constructing clique-structured hypernetworks³³. Given a simple network (:N) (e.g., a power-law randomized network), the clique-structured hypernetwork construction method converts the simple network into a clique-structured hypernetwork defined on the same set of nodes by identifying all the complete subgraphs (cliques) as hyperedges. However, since the cliques rely on the original links between nodes, the node relationships expressed by cliques fail to break the limitation of the simple network structure. The clique-structured hypernetwork is prone to form a larger number of small-size hyperedges that are scattered and cluttered. Therefore, we adopt the method of merging cliques to simplify the hyperedge. Once all cliques in the simple network are identified, a merging process based on overlap ratios is initiated. The overlap ratio between clique (:{C}_{1}) and clique (:{C}_{2}) is given by: (:frac{|{C}_{1}cap:{C}_{2}|}{|{C}_{1}cup:{C}_{2}|}). Each pair of cliques with overlap ratio exceeding a specified threshold is merged into a new hyperedge. This process continues until no pairs exceed the threshold or the target number of hyperedges is reached. Pairs of cliques with high overlap ratios indicate strong interconnections among their nodes, suggesting that these nodes likely belong to the same social group. By merging these cliques into a single hyperedge, the hypernetwork captures the underlying community structures more effectively. This method preserves original node relationships while disrupting conventional information pathways, including those formed by interest groups or platform recommendations. As a result, it offers a more nuanced understanding of node interactions and improves analytical capacity for dissemination modelling. In this way, we construct the desired hypernetwork (:H=(V,E)) from a simple network (:N). The node set (:V) denotes the users in the online social network and the edge set (:E) consists of hyperedges connecting the user nodes.

Figure 1 illustrates two types of hypernetworks constructed from a simple network containing 10 users and 10 edges. Simple edges and cliques represent similar node-connected edge relationships, while hyperedges can represent node relationships that are not captured by simple edges and cliques. For example, in Fig. 1b, node 5 is directly connected to nodes 3, 8, and 9. It is also connected to nodes 3, 4, and 7 by hyperedge (:{e}_{2}), as well as to nodes 6, 8, and 9 by hyperedge (:{e}_{3}). Thus, even though node 5 is not directly connected to nodes 4, 7, and 6 in the simple network, it interacts with these nodes through the hyperedges.

Assuming that (:M) is the size of current clique sets, it is necessary to traverse all (:frac{Mleft(M-1right)}{2}) clique pairs with a time complexity of (:O(M^{2})). In the worst case, the merge process needs to be performed (:M:)times, so the overall time complexity is about (:Oleft({M}^{3}right)). This method is suitable for small clique sets (smaller (:M)). For larger graphs, a combination of heuristic strategies or approximation algorithms is required to reduce the complexity. The merging threshold determines the level of clique aggregation. As seen in Table 1, we evaluate the sensitivity of this parameter by varying merging threshold across multiple values and examining its impact on hyperedge statistics. A lower threshold indicates a lower merging requirement, resulting in larger hyperedges but fewer total hyperedges. A higher threshold preserves smaller hyperedges. When the merging threshold (:=0.7), the hyperedge structure agrees with the original cluster number. Moreover, to evaluate the computational scalability, we test the model on networks of varying sizes (500, 1 K, 10 K, 30 K, 50 K, 100 K nodes) and measure runtime efficiency. Results indicate that while moderate-sized networks complete within seconds, larger networks require optimized implementations, such as approximate merging heuristics or parallel computing, to maintain scalability. At 50 K nodes, the computational burden escalates, and for 100 K nodes, computation time exceeds 12 h, making efficiency optimizations crucial. Fewer cliques are merged at higher thresholds, resulting in less computation time. Therefore, adjusting the merging threshold allows control of the balance between the granularity of the hypernetwork and computation cost, adapting it to the size and complexity of different networks.

Hypernetwork-based topic dissemination model for online social network

Individual state transition process

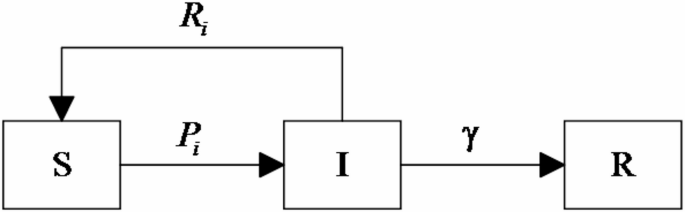
This subsection introduces a Hypernetwork-Based SIRS model (HSIRS), which includes three states: Susceptible (S), Infected (I), and Recovered (R), representing potential participants, active participants, and immune individuals, respectively. The state transition process in HSIRS model is illustrated in Fig. 2.

When a new topic enters the hypernetwork, the specific dissemination process unfolds as follows:

1. (1)

   Initialization: In the initial hypernetwork, there are I0 nodes in the initial infected state, spreading the topic by posting, commenting, etc. All other nodes are in the susceptible state S.

2. (2)

   State Update: At each time step, the state of all individuals is updated synchronously. When a susceptible node (:i) has an infection probability (:{P}_{i}) that exceeds its infection threshold (:{r}_{i}) (i.e., (:{P}_{i}>{r}_{i})), the node transitions from the susceptible state S to the infected state I. Infection threshold refers to the minimum force needed to change an individual’s behavior³⁸. In actual transmission process, there are differences between individuals who possess different infection threshold. Nodes in I-state transition to an immune state R at a certain recovery rate (:gamma:), meaning that they no longer engage in topic dissemination. Alternatively, they may maintain a level of activity and, with a re-entry probability (:{R}_{i}), return to the susceptible state S, indicating multiple participations in topic dissemination.

3. (3)

   Steady State: As the topic propagates through the hypernetwork, the states of nodes gradually stabilize and the system approaches a steady state, marking the end of topic dissemination.

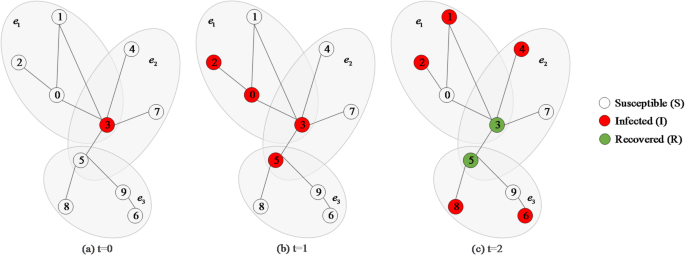
An example of the dissemination process of HSIRS model is given in Fig. 3. At (:t=1), nodes 2 is infected by node 3 via the hyperedge (:{e}_{1}), despite having no direct connection with node 3 in the simple network. At (:t=2), node 6 is infected by node 5 through the hyperedge (:{e}_{3}). The example demonstrates how the hypernetwork represents the complex interactions within multiple nodes, enhances network connectivity, and provides a deeper understanding of the topic dissemination mechanisms in complex social networks.

HSIRS topic dissemination model

The model assumes that the key factors influencing the node (:i)’s participation in topic dissemination are:

1. (1)

   Topic Attractiveness (:lambda:): The spread of a topic is constrained by its macro characteristics, such as validity, richness, and novelty. The parameter (:lambda:) quantifies the attractiveness of the topic based on its macro characteristics, with a value ranging from (:left[text{0,1}right]).

2. (2)

   Topic Sensitivity (:{S}_{i}): This parameter quantifies the level of interest and reaction of a node to various topics. For instance, nodes interested in technology will be more likely to participate in discussions related to new technological advancements, while they may be less inclined to engage with topics related to entertainment. To formalize this concept, we define two label vectors: node tag vector (:U={{u}_{1},{u}_{2},dots:,{u}_{n}}), representing the interest tags associated with a node, and topic tag vector (:T={{t}_{1},{t}_{2},dots:,{t}_{n}}), representing the tags associated with a topic, where (:n) is the number of tags. Topic sensitivity of node (:i) to a topic is defined as (:{S}_{i}=frac{2text{*}left|{T}_{tags}cap:{U}_{tags}right|}{left|{T}_{tags}right|+left|{U}_{tags}right|}), ranging from (:left[text{0,1}right]).

3. (3)

   Individual Activity (:{A}_{i}): Activity influences the rate at which nodes receive and disseminate information. Highly active nodes engage more frequently in discussions, increasing their exposure to new topics and their likelihood of dissemination. The parameter (:{A}_{i}) is used to analyze the impact of node (:i)’s activity level on topic dissemination, taking the value range of (:left[text{0,1}right]).

4. (4)

   Hyperedge Size Effect (:{tau:}_{k}): Hyperedges represent higher-order interactions, enabling complex association patterns beyond simple pairwise interactions and increasing the influence range of nodes within the hypernetwork. The size of a hyperedge plays a crucial role in topic dissemination, as larger hyperedges include more participants, increasing the potential audience for a topic. We consider the heterogeneous effects of different hyperedge sizes on topic dissemination. A weight (:{tau:}_{k}) is assigned to each hyperedge of size (:k) ranging from (:left[text{0,1}right]). Larger hyperedges allow more widespread dissemination, as they connect more nodes in a single interaction. The dissemination process prioritizes nodes in larger-size hyperedges, reflecting their greater influence in spreading topics. Smaller hyperedges, while still facilitating dissemination, may be more constrained in reach.

Based on the analysis above, HSIRS model is formulated to represent how nodes participate in new topics within the hypernetwork over time. Let (:t) be the time elapsed since the topic arose. The infection rate, representing the probability of a susceptible node (:i) participating in topic dissemination, is calculated as follows:

In Eq. (1), (:{N}_{i}) is the number of neighboring nodes of node (:i). (:stackrel{-}{{tau:}_{j}}=frac{sum:_{m=1}^{M}{tau:}_{{k}_{m}}}{M}) is the average weight over (:M) hyperedges involving node (:j) where each hyperedge (:m) has a size (:{k}_{m}). The symbol (:{delta:}_{j}) is an indicator function representing whether neighboring nodes are propagators: (:{delta:}_{j}left(tright)=left{begin{array}{c}0,:j=”I”:1,jne:”I”end{array}right.).

Additionally, individual activity (:{A}_{i}) influences the likelihood of a node participating in topic dissemination multiple times. Nodes with high activity are more likely to pay continuous attention to the progress of a certain topic and have a higher probability of engaging in the topic dissemination process many times. A generalized Pareto distribution is introduced to describe the trend of node participation in topic dissemination. As shown in Eq. (2), (:{R}_{i}left(varDelta:tright)) represents the re-entry rate of infected node (:i) where (:varDelta:t) denotes the time step. As (:varDelta:t) increases, the effect of individual activity decreases, reducing the probability of continuous participation:

According to the assumptions and state transfer probabilities of HSIRS model, the dissemination process algorithm is designed, and the specific steps are shown in Algorithm 1. The algorithm is structured into two primary components:

1. (1)

   Initialization: Parameters are set and initial topic propagators are generated.

2. (2)

   Iteration Loop: The process continues until a maximum iteration count is reached or no I-state nodes remain. During each iteration, the state of each node in the hypernetwork is evaluated based on its state and the corresponding actions are performed.

The time complexity of HSIRS model is determined by three key factors: time step iteration, node traversal and neighboring nodes computation. In the worst case, the time complexity of the algorithm is(::O(TN^{2})), where (:T) is the maximum simulation time step and (:N) is the total number of network nodes. In practice, the complexity may be reduced if the network is sparser.

This section aims to verify the influence of the aforementioned parameters on topic dissemination in hypernetworks. We conduct simulations and experiments on three constructed simulated networks and three real-world networks. The performance of HSIRS model is compared and analyzed against two existing dissemination models. In all subsequent simulations, the time step is set as (:varDelta:t=1) and a random infection threshold (:{r}_{i}) is assigned to each node.

Simulation results and analysis

To evaluate the effectiveness of HSIRS model, we simulate the dissemination effects using three network models: (1) BA Scale-Free Network: Using the Barabási-Albert (BA) model with a preferential attachment of (:m=4), we construct a network with (:N=500) nodes and an average degree (:stackrel{-}{k}=8), (2) WS Small-World Network: The Watts-Strogatz (WS) small-world network is generated by assigning each node five neighbors and a rewiring probability of 0.3, resulting in a network size of (:N=500) with an average degree (:stackrel{-}{k}=4), (3) ER Randomized Network: The Erdős-Rényi (ER) random network model, where each pair of nodes is connected with equal probability, is used to create a network of size (:N=500) with an average degree (:stackrel{-}{k}=9). After detecting and extracting all clique information, cliques are merged with a 0.1 merging threshold to construct hyperedges for the three simulated networks respectively. The final network structures are shown in Table 2, which is used for subsequent simulation and analysis.

Hypernetwork structure effects

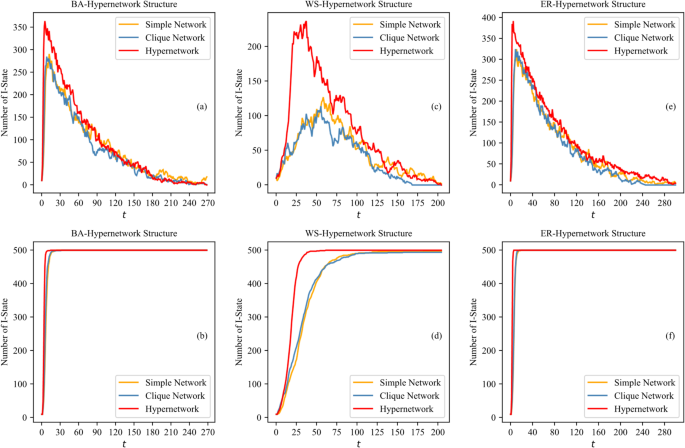
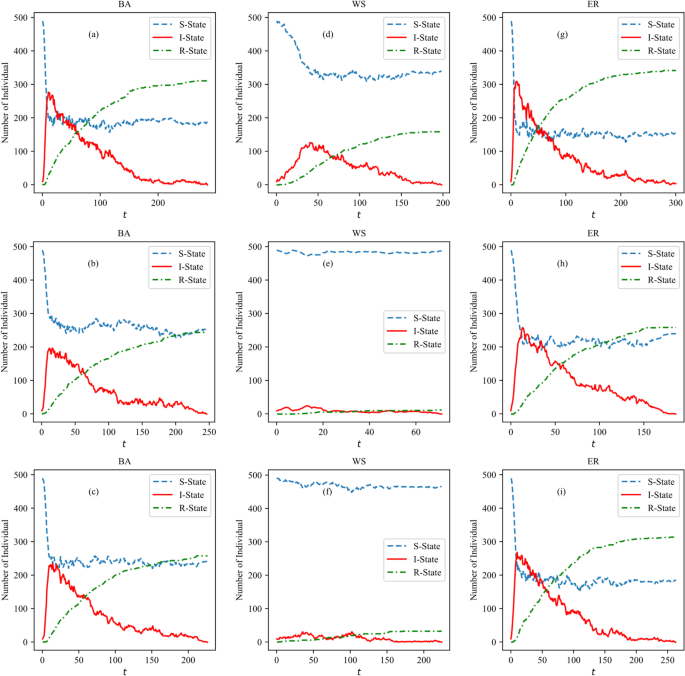
User relationship structures in online social networks substantially influence interactive behaviors and determine topic dissemination pathways. We simulate the topic dissemination for the three structures with initial conditions as follows: topic attractiveness (:lambda:=0.5), individual activity (:{A}_{i}=0.7), topic sensitivity (:{S}_{i}=0.5), recovery rate (:gamma:=0.02), fixing the initial topic propagators. The process and range results are presented in Fig. 4.

Figure 4 shows the dissemination simulation results across three network structures. Figure 4a, c,e show the dissemination process and Fig. 4b, d,f show the dissemination range overtime. Overall, topic dissemination processes under the simple network and the clique-structured hypernetwork exhibit similar characteristics with dissemination speed and peak infection. Under the hypernetwork constructed in this paper, topic dissemination is enhanced in speed and peak level, as hyperedges enable multipoint concurrent dissemination, where multiple nodes connected by hyperedges can simultaneously receive and transmit information. This effect is especially pronounced in the WS network with short average paths. In the BA network, the centralized structure causes hyperedge effects to focus mainly on a few highly connected nodes. These dominant nodes control the dissemination process, reinforcing the existing hierarchy. In the ER network, with its random connectivity, hyperedges has not greatly altered the information dissemination pattern. Therefore, hyperedges have limited effects on the overall dissemination dynamics in the BA and ER networks.

Reorganizing cliques into hyperedges changes the network topology, highlighting the hyperedge effects on topic dissemination. Hyperedges improve users’ access to topics, enabling faster and wider dissemination. Unlike simple networks, where influence is limited to direct neighbors, the hypergraph-based model captures complex interactions, simulating topic spread more effectively. Consequently, the hypernetworks formed by merging cliques are used for all subsequent experiments.

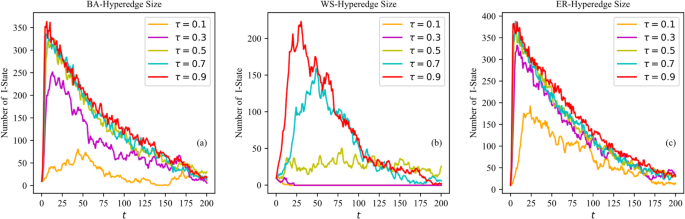
Hyperedge size effects

Nodes can simultaneously belong to multiple hyperedges of varying sizes, potentially impacting the dissemination process differently. To parameterize this influence, we consider the average hyperedge size effect, with values (:tau:=0.1,:0.3,:0.5,:0.7,:0.9,:lambda:=0.7,{A}_{i}=0.7,:{S}_{i}=0.5,gamma:=0.02).

Figure 5 illustrates the effects of varying (:tau:) values on topic dissemination across different hypernetworks. The WS hypernetwork exhibits high sensitivity to (:tau:) changes, while the ER hypernetwork remains stable. In the WS hypernetwork, smaller hyperedge sizes and short paths limit effective dissemination. At (:tau:le:0.3) topic spread is nearly suppressed. The higher volatility of the WS network reflects the dissemination is easily affected by the change of the hyperedge, and thus its robustness is relatively poor. Results in the BA and ER hypernetworks show weakened dissemination at (:tau:=0.1). In the BA hypernetwork, hub nodes sustain dissemination despite smaller hyperedges. The ER hypernetwork’s random connections still provide sufficient dissemination paths, allowing topic to spread even at low (:tau:) values. At (:tau::ge::0.5), dissemination curves in the BA and ER hypernetworks show little difference. Under different hyperedge sizes (τ), the BA network and ER network show lower volatility and relatively stable dissemination range, indicating their high robustness in the dissemination process.

These results highlight the adaptive capacity and dissemination of different hypernetworks in response to hyperedge size effects. Smaller hyperedge sizes tend to suppress dissemination and larger sizes enhance it. In the BA and ER hypernetworks, effects of hyperedge sizes eventually diminish, such that further increases in hyperedge size no longer improve the dissemination process beyond a certain level.

Topic sensitivity effects

The higher similarity between node tags and topic tags has, the higher sensitivity of users to topic is, increasing the probability of participation and dissemination. Three experiments are conducted on each simulated hypernetwork, with topic tags generated randomly and values

.

Figure 6 shows the topic dissemination simulation results on the simulated BA hypernetwork, WS hypernetwork, and ER hypernetwork three times respectively. Results in the ER hypernetwork exhibit the highest infection count and largest dissemination speed, but topics quickly diminish. The WS hypernetwork, with the smallest average node hyperdegree and lowest density, shows the slowest and minimal spread of new topics. All three simulated hypernetworks exhibit noticeable volatility and long-tail effects, maintaining sustained attention and engagement long after the initial peak.

Topic sensitivity of nodes varies for different topics, leading to different dissemination speeds and fluctuations. In comparing the three experiments, the first experiment generated a topic that considerably stimulated node participation, while the second encountered lower node sensitivity and weaker dissemination. The observed variability in dissemination patterns within the same hypernetwork suggests no direct correlation between node sensitivity and hyperdegree. Therefore, the scope and speed of topic dissemination are influenced by network structure and closely related to individual characteristics, such as node sensitivity to topics.

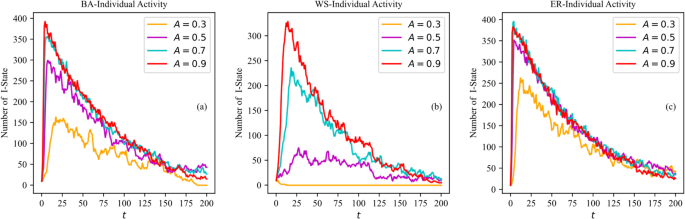
Individual activity effects

Individual activity impacts node acquisition and participation in new topic dissemination. With parameters set as (:lambda:=0.7,:tau:=1,::gamma:=0.02), and fixed initial propagators and topic tags, Fig. 7 illustrates the topic dissemination curves in the simulated hypernetworks at various individual activity levels (:A=0.3,:0.5,:0.7,:0.9).

Higher node activity correlates with faster and more extensive topic dissemination. At a low activity level ((:A=0.3)), topics are easily ignored with minimal node participation, while at a high activity level ((:A=0.9)), nodes quickly engage, leading to a rapid increase in infections. The WS hypernetwork, with its small-world characteristics, exhibits high sensitivity to activity level changes and poor robustness, affecting topic dissemination greatly. In contrast, the ER hypernetwork, with fewer clusters and short paths, shows less sensitivity to activity variations and high robustness, resulting in less pronounced increases in dissemination speed and scale even at higher activity levels. Highly active hypernetworks enable swift topic spread and robust dissemination fluctuations due to high re-entry probabilities of active nodes, which aligns with the observation that such nodes consistently engage in topic dissemination.

Statistical significance tests

ANOVA analysis of I-State curves across different experimental groups (Table 3) reveals that network structure, hyperedge size, and individual activity significantly impact infection dynamics across all network types. WS networks exhibit the strongest effects, indicating that topological characteristics accelerate topic dissemination. Hyperedge size has a particularly significant influence ((:text{p}approx:0)), with larger hyperedges leading to faster and wider dissemination. Individual activity also plays a key role, as highly active individuals enhance topic propagation. Notably, topic type has no significant effect in BA networks ((:text{p}=0.35066)) but does influence dissemination in WS and ER networks, suggesting that network structure determines sensitivity to different topics. Overall, these findings confirm that hypernetwork structure and individual behavior significantly shape topic dissemination, validating the improved model.

Real-world network experiment results and analysis

To evaluate the effect of HSIRS topic dissemination model on real-world networks, we conducted experiments on three distinct social networks: (1) Weibo Social Network (https://github.com/WxxShirley/WeiboSpammer): constituting 903 nodes and 2,065 edges, representing real users on the Weibo platform. (2) Twitter Network (https://snap.stanford.edu/.

data/twitter.tar.gz): comprising 236 nodes and 1,811 edges from the social database of Twitter. (3) Facebook Network (https://snap.stanford.edu/data/facebook.tar.gz): containing 333 nodes and 2,519 edges, obtained from Stanford University database. All clique information is extracted and the cliques are merged with a 0.1 merging threshold to construct the hypernetworks for the three real-world networks respectively. The specific information is shown in Table 4.

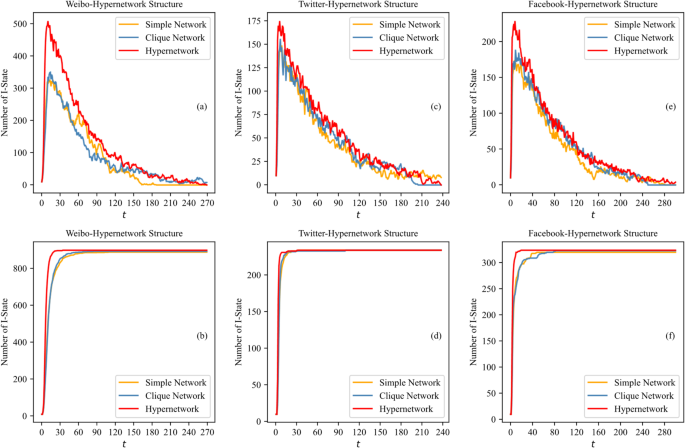
Hypernetwork structure effects

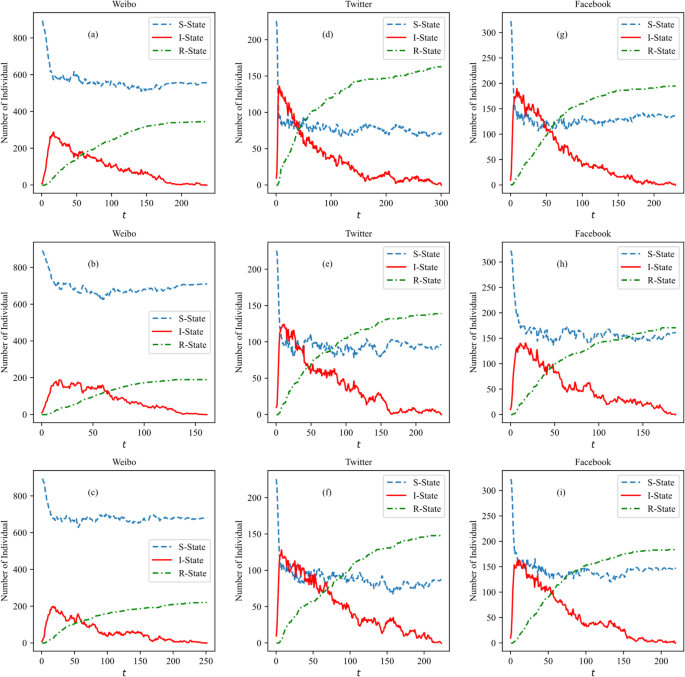
Figure 8 shows the topic dissemination results across three network structures within three real social networks with values (:lambda:=0.5,:{A}_{i}=0.7,:{S}_{i}=0.5,:tau:=1,gamma:=0.02), illustrating comparative dissemination outcomes on each platform.

Weibo network exhibits a mix of small-world and partially random network characteristics, presenting local aggregation and short path lengths. Twitter network is primarily based on follower relationships, tending towards scale-free network characteristics. Facebook network emphasizes personal relationships, resulting in a highly aggregated community structure and strong distributed characteristics.

Dissemination patterns in real networks align with those observed in simulated networks, demonstrating the robustness of HSIRS model in capturing real network dynamics. Early-stage infection curves peaking concurrently in both simple networks and clique-structured hypernetworks. Hyperedge effects are more pronounced in Weibo and Facebook networks due to their small-world characteristics, while dissemination in Twitter network resembles a scale-free network. The results also reveal that clique connections function similarly to simple edges, limiting the impact of clique-based hyperedges. Hyperedges constructed in this paper connect a broader set of nodes, enhancing multiple interactions and promoting more robust topic dissemination. This mirrors real-world online social network behaviors, involving one-to-one information dissemination with direct friends and multiple interactions through interest groups or platform recommendations.

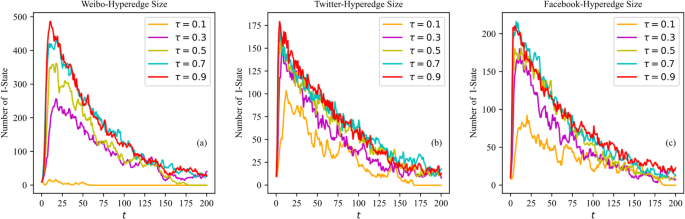
Hyperedge size effects

Figure 9 displays the results of topic dissemination in real hypernetworks with varying hyperedge size effect parameters (:tau:=0.1,:text{0.3,0.5,0.7,0.9}) and values (:lambda:=0.7,{A}_{i}=0.7,:{S}_{i}=0.5,gamma:=0.02), showing similarity to those in the simulated networks that the performance of the model remains stable for different (:tau:). In Weibo hypernetwork, when (:tau:=0.1), topics have limited range and persist for only 50 time steps. As (:tau:) increases, dissemination reaches a higher peak at a faster rate and lasts longer. In Twitter and Facebook hypernetworks, an increase in hyperedge size positively impacts topic dissemination when (:tau:le::0.7), but gradually inhibits it when (:tau:>:0.7). Facebook hypernetwork achieves its strongest dissemination at (:tau:=0.7) rather than (:tau:=0.9). Results suggests that the model robustly captures the decreasing effect of hyperedge size on dissemination efficiency, highlighting the complex role of hyperedge size in real networks.

Results also reveal that large communities have advantages in topic dissemination. However, excessive user participation in large communities can lead to information overload or choice fatigue and inhibit topic dissemination effectiveness.

Topic sensitivity effects

Figure 10 shows the experimental dissemination results of different topics in real hypernetworks with values (:{A}_{i}=0.7,lambda:=0.5,tau:=1,:gamma:=0.02,:{S}_{i}=frac{2*|{T}_{tags}cap:{U}_{tags}|}{left|{T}_{tags}right|+left|{U}_{tags}right|}). Topic characteristics are represented by 3 to 5 interest labels, randomly selected from those assigned to nodes.

In real social networks, topic dissemination follows similar patterns: rapid initial growth, high volatility, and sustained node engagement. Weibo hypernetwork’s sparse structure contrasts with the denser and more interconnected Twitter and Facebook networks, which facilitate faster topic spread. Varying node sensitivity to topics leads to diverse dissemination outcomes.

Individual activity effects

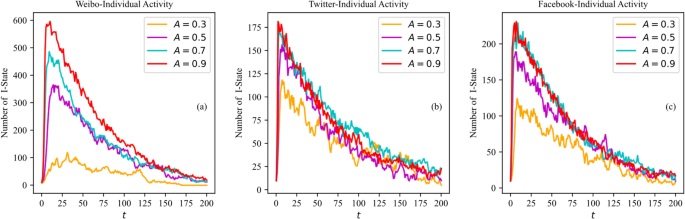
Figure 11 illustrates how varying individual activity levels impact topic dissemination in real social networks with values (:A=0.3,:0.5,:0.7,:0.9,::lambda:=0.7,tau:=1,::gamma:=0.02.) The sensitivity of individual activity levels to topic dissemination further demonstrates the robustness of HSIRS model in real networks. Result in real hypernetworks align with simulated hypernetworks, showing that increased activity levels enhance dissemination effects. In Weibo hypernetwork, activity levels have a pronounced effect due to its lower average node hyperdegree and dispersed community structure, where structural relationship exerts a weaker influence. Higher individual activity levels improve topic dissemination efficiency and sustain attention over time across communities.

Statistical significance tests

ANOVA analysis of I-State curves across different real-world network experimental groups (Table 5) shows that network structure, hyperedge size, and individual activity significantly influence topic dissemination across Weibo, Twitter, and Facebook. Among them, Weibo exhibits the strongest effects, suggesting that its local clustering and short paths accelerate information diffusion. On Twitter, individual activity plays a dominant role, indicating that popular users drive dissemination. Facebook, with strong community aggregation, remains significantly influenced by network structure and individual activity, but topic type has no significant effect, suggesting that content matters less in closed communities. Compared to simulated networks, hyperedge size remains a significant factor in real networks, reinforcing the effectiveness of the hypernetwork approach in modeling real-world information spread.

Comparative analysis of different models

This subsection compares HSIRS model with CSIRS and Bodó-SIS models. Experimental settings from the literature were applied to the simulated BA network and real Twitter network. Parameter settings from the literature were used, and the results are shown in Figs. 12, 13 and 14.

Considering different network construction methods, topics, and individual characteristics, the topic dissemination models display varying patterns and effects. HSIRS model shows the most consistent and effective topic dissemination across both simulated and real networks and the scale-free characteristics of Twitter hypernetwork further validate its reliability. CSIRS model considers individual and topic heterogeneity in simple networks, but it struggles with higher-order interactions, leading to rapid rises and declines and shorter topic lifespans. Bodó-SIS model extends infectious disease model to hypergraphs through clique-based hyperedges and fails to accurately reflect real-world topic dissemination, displaying slow initial growth and long-term constant number of infections.

Statistical significance tests

The I-State curve results of the three models were analyzed using t-tests. As shown in Table 6, HSIRS differs significantly from CSIRS and Bodó-SIS on both the BA and Twitter networks ((:text{p}approx:0)). The t-value for HSIRS and CSIRS is higher, indicating that HSIRS, with its improved dissemination mechanism, better captures the effects of individual characteristics, topic characteristics, and network structure. While HSIRS also differs significantly from Bodó-SIS, the smaller difference suggests that Bodó-SIS can partially simulate propagation but remains less effective than HSIRS. Overall, HSIRS outperforms existing models across different network environments, confirming its improvements.

This paper aims to depict topic dissemination dynamics within real online social networks by incorporating hypergraph theory. The proposed HSIRS model, based on the SIRS framework and considering hyperedge size, user sensitivity, and individual activity factors, provides a comprehensive analysis of global topic dissemination. Experimental results indicate that HSIRS model outperforms other models in simulated and real-world social networks, offering more expansive and rapid topic dissemination. Factors such as hyperedge size, topic content, hyperdegree value, and user activity level have varying effects on the speed, peak value, and duration of topic dissemination.

Theoretically, hyperedge topology influences dissemination dynamics. Larger hyperedges accelerate spread by enabling simultaneous transmission to multiple nodes, while smaller ones may constrain dissemination. The heterogeneity of hyperedges, including variations in user connectivity and interests, further affects dissemination efficiency. Compared with traditional pairwise networks, hypergraphs capture nonlinear diffusion patterns, reflecting real-world social interactions where information spreads through group-based rather than sequential connections. HSIRS model aligns with empirical trends in viral content dissemination and social influence theories. Social media platforms exhibit rapid, large-scale information spread driven by network structure and influential users. Our findings support this, demonstrating that highly active individuals and densely connected hyperedges enhance dissemination. The limited effect of topic type in certain networks suggests that structural properties and individual behavior often play a more decisive role than content characteristics in viral diffusion. Moreover, the robustness and reliable performance of HSIRS model across different network topologies, hyperedge configurations and user activity levels ensure that it is equally valid in real networks, providing a useful tool for understanding topic dissemination in complex social networks. These results can be utilized to predict and manage public opinion on various topics. By monitoring large-scale communities and active users, strategically placing relevant content, and guiding the influence of key individuals, it is possible to effectively control the spread of topics, which can also help curb the dissemination of harmful information and mitigate extreme behaviors.

Topic dissemination in online social networks is inherently complex. Future research could build on this paper by exploring user interaction patterns, creating a generalized generative model for hypernetworks and examining the structural impacts on dissemination. Additionally, this paper assumes a constant number of nodes in the hypernetwork, which does not fully reflect the dynamic nature of online social networks in real world. Incorporating population mobility in future models will provide a more comprehensive representation of the topic dissemination process.