Main

The microbiome is known to play a role in many human phenotypes8. In turn, diet, medications, lifestyle and environmental exposures affect microbiome composition5,9,10. As few bacterial components of the microbiome survive for very long outside the human body, most must somehow be acquired from other humans through physical contact. Although maternal transmission is one obvious pathway6,11,12, adults may acquire microbial species from other people beyond their mothers via social interactions1. Indeed, in models involving both mice and primates, gut microbiome information can predict a host’s social interactions2,13,14,15,16,17,18. In humans, recent evidence indicates the salience of household and spousal transmission1,3,4. Yet, a substantially broader set of social relationships that people have—including in particular to unrelated people residing outside a person’s household—and the details of those social interactions (for example, their duration or frequency), are also likely relevant to a person’s microbiome composition.

Study cohort and network mapping

We studied 1,787 adults in 18 isolated villages in Honduras who are part of a larger population-based cohort7. This is a traditional setting involving face-to-face interactions within a circumscribed population that partakes of a traditional diet and is relatively devoid of antibiotics and other medications. The average distance from each of the 18 villages to the nearest other village among the 18 is 1.1 km, and the average distance to the farthest other village is 24.7 km. The populations of these 18 villages range in size from 66 to 432 people, and their underlying average household size is 3.49. The average age of participants is 41 years (s.d. = 17; range, 15–93); 62% are women and 41.8% are married.

We sociocentrically mapped face-to-face social networks for whole villages at two time points, collected a comprehensive set of individual and community-level characteristics, and obtained detailed gut microbiome sequencing data. The percentage of people in the village-level social networks for whom microbiome samples were collected ranged from 43% to 76% (Supplementary Table 2). We collected microbiome data for all 18 villages in 2020 and again for 4 of these villages (n = 301 people) roughly 2 years later. Both social network data19,20 and microbiome data21 from such developing-world settings are scarce.

To map the social relationships within each village, we asked questions such as “With whom do you spend free time?” and “Who do you trust to talk about something personal or private?” (Supplementary Table 1). The total number of relationships identified within our cohort were: partner/spouse (410), father (303), mother (594), sibling (1,059), child (427), close friends (1,627), spend free time (1,749), and personal or private conversation (1,902). Some of these relationships overlap, and, after network symmetrization, we identified 4,658 unique social network links. For people who report spending free time together, we also collected details such as how often they did so, whether they shared meals, and how they greeted each other. The networks were mapped roughly in 2019.

Microbiome profiling

Microbial species can have materially divergent strains22 and genetically distinctive strain-sharing between two people can offer suggestive evidence that the shared strain resulted from interpersonal transmission rather than common exposure to an environmental factor such as diet (for example, fermented foods)4,22,23,24,25.

We performed strain-level profiling with StrainPhlAn4 and detected putative transmission events between pairs of people26. We summarized the strain-level similarity between two people with a strain-sharing rate metric that is equal to the number of shared strains divided by the number of species with available strain profiles that are present in any two samples27. Overall, our data included information on 2,543 species and 339,137 strains (from the 841 species profiled by StrainPhlAn). We summarized the species-level beta diversity using the Bray–Curtis dissimilarity and the Jaccard index calculated on relative abundances.

Dimensionality reduction of the species-level relative abundances reveals differences in composition for most two-village comparisons and across all the villages combined (Extended Data Fig. 1).

Strain-sharing across relationship types

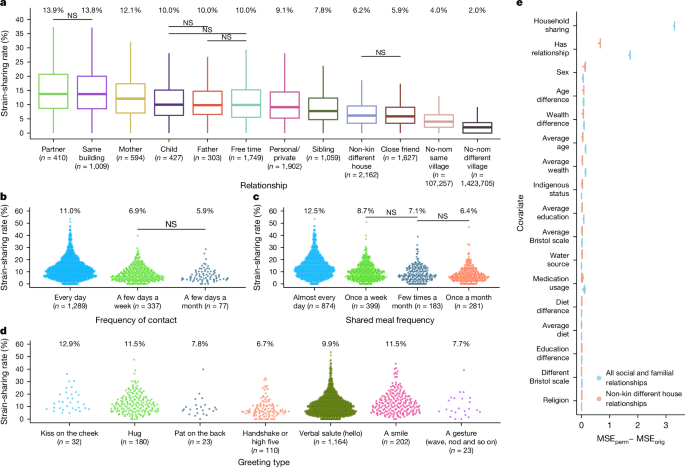
Pairs of people with diverse sorts of relationships (spouse, father, mother, sibling, child, close friend, free time, personal or private conversations) share significantly more microbial species and strains with each other than other pairs of people from within the same village with no relationship, and we observe a gradient of strain-sharing among relationships (two-sided Wilcoxon rank-sum tests, maximum adjusted P value (max Padj) ≤ 0.05) (Fig. 1a). We find that the presence of a relationship tie, no matter whether to family or friend, increases the likelihood of strain-sharing (linear mixed-effects regression, all relationships β = 2.912; P < 2 × 10−16, and non-kin relationships β = 3.134; P < 2 × 10−16). Using a covariate permutation approach, it is apparent that the presence of a tie between two people has a larger association with strain-sharing than the similarity between the two people with respect to other factors such as diet, medications or socio-demographic attributes (Fig. 1e and Supplementary Data 1).

Fig. 1: Strain-sharing across multiple relationship types.
figure 1

a, Distribution of strain-sharing rates based on relationship type. All pairwise relationship comparisons are significantly different, except for those marked NS (Kruskal–Wallis test, χ2 = 65,983; n = 1,542,204, P < 2.2 × 10−16; two-sided Wilcoxon rank-sum tests for pairwise comparisons). The final two boxes quantify the strain-sharing rates between all pairs of people living in the same village without a nominated relationship (nom) and all pairs of people living in different villages, respectively. Data are represented as boxplots, where the middle line is the median and the lower and upper hinges correspond to the first and third quartiles. The whiskers extend from the hinge to the largest or smallest value no further than 1.5× IQR from the hinge. The median values for each distribution are also reported at the top of each box. b, The propensity to share strains increases as a function of how often a pair spends free time together. Only non-significant pairwise comparisons are indicated (Kruskal–Wallis test, χ2 = 105.46, n = 1,703, P < 2.2 × 10−16; two-sided Wilcoxon rank-sum tests for pairwise comparisons). c, The propensity to share strains increases as a function of how often a pair shares meals together. Only non-significant pairwise comparisons are shown (Kruskal–Wallis test, χ2 = 194.25, n = 1,737, P < 2.2 × 10−16; two-sided Wilcoxon rank-sum tests for pairwise comparisons). d, Strain-sharing rate varies by the typical way people greet each other (Kruskal–Wallis test, χ2 = 40.03, n = 1,734, P = 4.47 × 10−7). e, We performed 1,000 permutations per covariate and used linear models to estimate the mean squared error in the permutations (MSEperm) and then compared the difference between the mean squared errors in the permutation models and the original model (MSEorig); as shown, the most important feature identified is the presence of a relationship (when looking at only the non-kin relationships). Data are presented as mean ± s.d. NS, not significant (Padj ≥ 0.05).

Full size image

Spouses and same-household relationships have the highest strain-sharing (median strain-sharing rate of 13.9% and 13.8%, respectively). While previous studies have documented potential household and familial transmission1,3,4, we also observe an elevated strain-sharing rate between non-kin relationships living in different households (median 7.8%, permutation P < 2.2 × 10−16). We observe less strain-sharing between people living in the same village who lack a social relationship (median 4.0%); this background rate might result from shared village environments or network-wide circulation of strains. We observe an even lower strain-sharing rate between people living in altogether different villages (median 2.0%).

Since species distributions are to some extent village-dependent (Extended Data Fig. 1), and pairs of people in the same village have a higher strain-sharing rate than pairs in different villages (Fig. 1a), village-level sharing can serve as a baseline for comparison. To account for both the potential influence of village-wide microbiome niches and of village-level network structure, we compared each relationship distribution to 100 samples from a within-village relationship permutation (for example, swapping mother–child pairs in the same village; Methods) and observed the same pattern of variation in strain-sharing by relationship type (Supplementary Fig. 1). This result is also observed at the species level (Extended Data Fig. 2 and Supplementary Fig. 2), although to a lesser extent, possibly suggesting that strain-sharing is more likely to be a result of direct transmission than species-level sharing, which could potentially originate from, say, a shared environment.

For people who report spending free time together, we examined how strain-sharing may relate to how often they spend free time together, how often they share meals and how they typically greet each other (Fig. 1b–d). The frequency that a person spends time with someone, whether in general or through a meal, is associated with an increase in strain-sharing (free time, Kruskal–Wallis test, χ2 =  105.45, n = 1,703; P < 2.2 × 10−16; meals, Kruskal–Wallis test, χ2 =  194.25, n = 1,737; P <  2.2 × 10−16). This result holds even when excluding the effect of kinship and living in the same house (free time, Kruskal–Wallis test, χ2 =  12.96, n = 620; P =  1.53 × 10−3; meals, Kruskal–Wallis test, χ2 =  10.6, n = 641; P =  0.014) (Supplementary Fig. 2), suggesting that close physical proximity and shared meals are potential transmission routes when people are not cohabiting. To be clear, shared meals can lead to similar gut microbiomes because eating similar foods at the same time can lead to microbial sorting in the gut, creating similar microbial communities even if there is no direct exchange of microbes between people28. In certain analyses below, we accordingly adjust for diet, medications, water source and so on.

Pairs of people who greet each other with a kiss on the cheek have the highest median strain-sharing rate (median 12.9%)—although, perhaps due to the low sample size and diversity of greeting types, the strain-sharing rates across most greeting types are not significantly different (Fig. 1d and Supplementary Fig. 3). The strain-sharing rate for the subsample of non-kin living in different households who spend free time together almost every day (median of 7.1%) is higher than the strain-sharing rate for such people who see each other only once a week (6.0%) or a few times a month (4.8%) (Extended Data Fig. 3). A similar gradient is observed with the frequency that non-cohabiting non-kin have meals together, with those having meals daily or weekly (median strain-sharing rate 6.9%) sharing more than those who have a meal together a few times or only once a month (6.3% and 5.9%). Finally, when the reciprocity of the relationship is considered (that is, both people need to nominate each other for the tie to be deemed present), we observed an increased strain-sharing rate in all relationship types (except for partner) (Extended Data Fig. 4).

We find that mothers have a significantly higher strain-sharing rate with their children than fathers (two-sided Wilcoxon rank-sum test, Padj ≤ 0.05) (Supplementary Fig. 4). Mothers may transmit bacterial strains to children during childbirth29, and this higher strain-sharing rate may be a result of the retention of strains transmitted during infancy (indeed, the younger the child is, the higher the strain-sharing rate between mothers and their children; Supplementary Fig. 4). The higher mother–child strain-sharing rate may also relate to cultural practices that result in more opportunities for household transmission between mothers and their (adolescent or adult) children.

In contrast to previous analyses1, we find no evidence that women are more likely to share strains with their direct social connections than men (two-sided Wilcoxon rank-sum test, Padj ≥ 0.05) (Supplementary Fig. 5). In fact, at the species level, we observe the opposite, whereby men are more microbially similar to their connections than women, based on Bray–Curtis dissimilarity (two-sided Wilcoxon rank-sum test, Padj ≤ 0.05; Supplementary Fig. 5). A large portion of this seems to stem from brothers having more similar microbiomes to each other than sisters (median Bray–Curtis dissimilarity 0.615 and 0.696, respectively; two-sided Wilcoxon rank-sum test, Padj ≤ 0.05; Supplementary Fig. 5). However, this does not appear with the Jaccard index, suggesting that the absolute difference in species between brothers and sisters is not large, but that sisters are more variable in their relative abundances than brothers. The contrast with previous work may relate to different social habits in Honduras (for example, compared with Fiji30) or to differences between the oral and gut microbiome.

Strain-sharing predicts relationships

To evaluate the strength of strain- and species-sharing across relationship types, we implemented a mixed-effects logistic regression model with cross-validation to predict whether any pair of people in a village has a social or familial tie. If there is a strong relationship between the social network and the microbiome network, we would expect the microbiome similarity between two people to be a strong predictor of a social tie. We also specified a second model that removed kin and household connections from our positive class. To account for potential confounding by socio-demographic factors, we created four versions of each model: with the strain-sharing rate as the only predictor (in addition to a random slope for each village); with only all the socio-demographic variables (that is, residing in the same household, age, sex, wealth, education, religion and indigenous status); with only strain-sharing rate and age and sex; and with strain-sharing rate and all the socio-demographic variables (Methods).

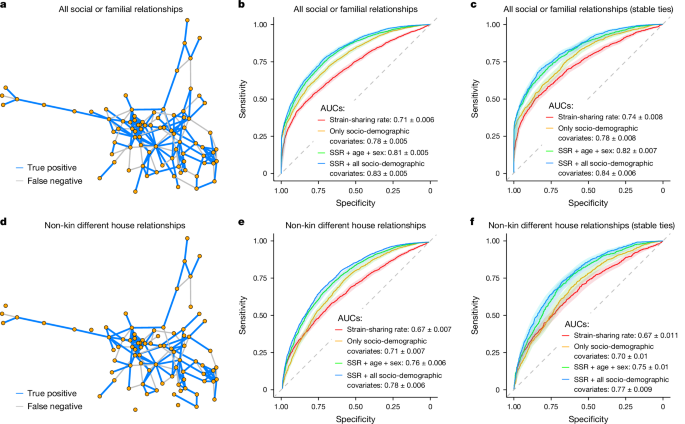
Using strain-sharing rate as the only predictor, the classifier achieves moderately strong performance across all relationships and also in non-kin, different-household relationships (area under receiver operating characteristic (ROC) curves (AUC) 0.71 ± 0.006 and AUC 0.67 ± 0.007, respectively) (Fig. 2b,e); Fig. 2a,d shows respective model predictions as applied to an illustrative village. Prediction performance is boosted when adding socio-demographic covariates, reaching AUC 0.83 ± 0.005 and AUC 0.78 ± 0.006 when predicting familial and non-kin relationships, respectively. Species-level similarity, as measured by Jaccard index or Bray–Curtis dissimilarity, achieves poor performance (all relationships: Jaccard, AUC 0.54 ± 0.008, Bray–Curtis, AUC 0.52 ± 0.008; Supplementary Fig. 6).

Fig. 2: Strain-level models predicting social connections.
figure 2

a,d, True-positive and false-negative network predictions for all relationships (a) and non-kin-different-household relationships only (d) for the village of Hernani (all relationships, n = 210; non-kin-different-household relationships, n = 165). As expected, the model including all relationships performs better than the non-kin, different-household model as there is increased sharing within households and amongst kin. The model also generally performs better at predicting within social clusters as there is increased strain-sharing around nodes with a high clustering coefficient. b,c,e,f, AUC predicting social or familial relationships (b), or non-kin-different-household relationships only (e), compared with un-nominated pairs living in the same village. When looking at stable ties across time (over a 2-year span), the AUC in both predictions remains stable and slightly improved in the strain-sharing-rate-only model (c and f). DeLong 95% confidence intervals are shaded surrounding each line. The diagonal dotted line indicates an AUC of 0.50, a ‘test’ no better than chance. Legends report the mean and s.d. for each classifier’s AUC. SSR, strain-sharing rate.

Full size image

We also performed two sensitivity analyses, involving stable ties and reciprocated ties. Using additional network data collected roughly 2.5 years earlier (in 2016), we selected a subset of ties that were classified as ‘stable’ if the participant previously reported the same connection. The stable tie classifier achieves similar performance when compared with the model run only on the second time-point social network on both all familial and social relationships (Fig. 2b,c) and on non-kin, different-household relationships (Fig. 2e,f). We also observed similar results when predicting relationship presence in the subset of strictly reciprocated ties (Supplementary Fig. 7 and Supplementary Table 3).

To understand how much more strongly strain-sharing indicates a social relationship compared with socio-demographic attributes, we again use permutation feature importance metrics (Methods)31, and we find that the strain-sharing rate is a stronger predictor of a relationship than similarity along any socio-demographic dimension (Extended Data Fig. 5).

Longitudinal analysis of strain-sharing

A subset of 301 people living in four villages were re-contacted after 2 years (roughly in 2021) and asked to provide a second stool sample. We first examined the fraction of strains retained over time by calculating the strain-sharing rate between pairs of samples provided by the same person; we observed a median value of 0.26 (interquartile range (IQR) 0.04–0.48) (a retention rate lower than other cohorts32).

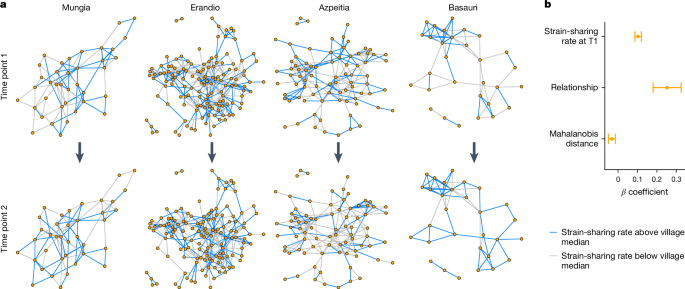
Then, by using the social network obtained at the outset (in 2019), we modelled the strain-sharing rate between pairs of (connected and unconnected) people in the same village at follow-up (Fig. 3; Methods). That is, we assessed how the existence of a tie between a pair of people, compared with the non-existence of a tie, was associated with any change in strain-sharing, comparing pairs of connected people with otherwise similar pairs of unconnected people in the same village 2 years later.

Fig. 3: Microbiome strain-sharing across two time points.
figure 3

a, Strain-sharing between pairs of people across two time points roughly 2 years apart in four villages (n = 301). A tie between two people is drawn if a relationship between them is discerned at time point 1, coloured in blue if the strain-sharing rate is above the median strain-sharing rate of the village at the first time point, otherwise grey. b, Standardized coefficients and s.e. (as bars) from the linear mixed-effect model; the primary coefficient of interest is for whether there is a ‘relationship’ (social connection) between the pair of people or not indicating that connected people come to share more strains over time than unconnected people in the same village (linear mixed model n = 14,268; two-sided Satterthwaite’s t-tests: strain-sharing rate at T1, P < 2 × 10−16; relationship, P = 7.6 × 10−12; Mahalanobis distance, P = 6.4 × 10−4).

Full size image

We observed that connected people have a higher strain-sharing rate at the subsequent time point than unconnected people (Fig. 3b). This was the case even after accounting for the socio-demographic (and dietary, medication and so on) similarity of the two people, their baseline level of strain-sharing and their village co-residence (Fig. 3b and Supplementary Data 2); that is, the coefficient associated with the existence of a previous relationship was positive (linear mixed-effects regression β = 0.25103; P = 8.28 × 10−11). Moreover, as expected, the coefficient associated with strain-sharing between pairs of people at the first time point was also positive (linear mixed-effects regression β = 0.1033; P < 2 × 10−16), and the coefficient for the socio-demographic dissimilarity of the two people at baseline, as measured by the Mahalanobis distance, was negative (linear mixed-effects regression β = −0.0318; P = 6.4 × 10−4) (see Supplementary Data 2 for more analyses). We obtained similar results when modelling sharing status for each individual species in pairs of people (across all species combined) or when using a model with separate socio-demographic variables (Supplementary Data 2; Methods).

Network position and strain-sharing

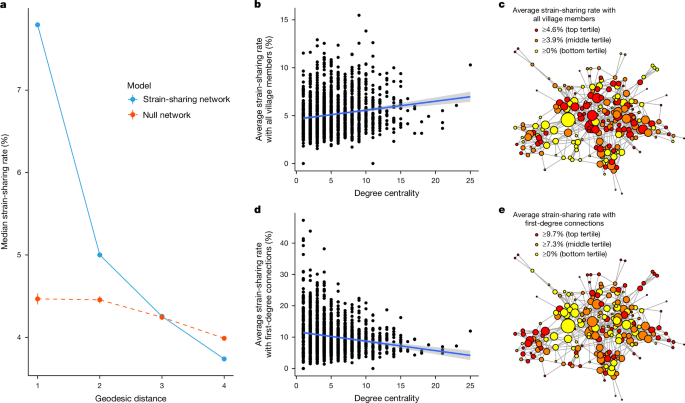
The observed strain-sharing patterns within villages may reflect potential chains of transmission. For example, if a person’s microbiome is more similar to that of their friends than expected under the assumption that microbiome distribution and social network structure are independent, is this similarity also present between friends of friends? To explore this, we can calculate the distribution of strain-sharing rates based on the shortest geodesic distance between two people. Under the null hypothesis that a person’s social network has no marginal relationship with their microbiome composition, we create a permutation-based null distribution by randomly reassigning microbiomes across people in the village, and then comparing the resulting strain-sharing rates by geodesic distance. First-degree relationships have a much higher strain-sharing rate than we would expect under the null hypothesis (median 7.95%). This effect also extends to second-degree connections (5.10%) before falling off at a social horizon of third-degree connections (4.35%), where pairs of people have a median strain-sharing rate no higher than would be expected under the null hypothesis (Fig. 4a) (see Supplementary Fig. 8 for species-level analyses).

Fig. 4: Strain-sharing and social network position.
figure 4

a, The strain-sharing rate by geodesic distance is shown. Null distributions were calculated based on 10,000 random samples from a within-village microbiome permutation. The null distribution slopes downwards because of the effect of large networks; larger villages have more pairs with a higher geodesic distance between them and, on average, a lower average strain-sharing rate between individual people (see Supplementary Fig. 10 for more details); 95% confidence intervals are plotted around the null distributions. People have more similar microbiomes to their first- and second-degree social connections that expected due to chance. b, As a person’s degree centrality (number of social connections) increases and they are more socially embedded in the village, their average strain-sharing rate with the village also tends to increase (Pearson correlation ρ = 0.16; P = 1.54 × 10−12 two-sided correlation test). The grey shaded area around the regression line represents the 95% confidence interval. c, Example social network for Hondarribia. People with more connections (degree) and a higher network centrality (betweenness or eigenvector) tend to be more microbially typical. Nodes are coloured according to their average strain-sharing rate with the rest of the village, and nodes are sized according to their degree centrality. d, When people have a wider variety of social connections (increasing degree centrality), between-host heterogeneity tends to increase, and people on average have a lower strain-sharing rate with their first-degree connections (Pearson correlation ρ = −0.18; P = 3.6 × 10−14 two-sided correlation test). The grey shaded area around the regression line represents the 95% confidence interval. e, Example social network for Hondarribia. People in the centre, with a wider variety of social connections, have, on average, a lower strain-sharing rate with their first-degree connections. Nodes are coloured according to average strain-sharing rate with first-degree connections, and nodes are sized according to degree centrality.

Full size image

The strain-sharing patterns we observe allow us to view microbiome strain-sharing from the framework of ecology. People who are more socially central in the network may also be more microbially central and more exposed to strains potentially spreading within a network. That is, we might expect that central people are more microbially related to the rest of the village and more representative of the social microbiome (that is, the microbial metacommunity of transmittable strains within the village). After controlling for covariates, we tested whether there was a relationship between a person’s microbiome centrality, measured by their average strain-sharing rate with others in the village, and their social network centrality (that is, degree centrality, normalized betweenness centrality, or eigenvector centrality).

All three measures of social network centrality were correlated positively with a person’s average strain-sharing rate to the rest of the village, indicating that the microbiome of more socially central people is more representative of the microbiome in the village (linear mixed-effects regression; degree, β = 0.046; P = 3.14 × 10−10; normalized betweenness, β = 6.27; P = 1.21 × 10−4; eigenvector, β = 1.27; P = 1.67 × 10−10) (Fig. 4b and Supplementary Data 3). This effect is apparent visually in Fig. 4c, where participants are coloured based on their average strain-sharing rate with the rest of the village; more socially central people tend to have higher strain-sharing rates with everyone else than socially peripheral people.

We may also suggest that, whereas socially central people are more microbially representative of the overall network, they may be less microbially similar to their own first-degree social connections. A very popular person may be more representative of the social group at large, but, as a result of their many social interactions, they may be more removed from each of their individual connections, in a paradox of popularity. Indeed, we observe that increases in all three social network centrality measures correlate with a decrease in average microbiome similarity to first-degree connections (linear mixed-effects regression; degree, β = −0.21; P = 1.92 × 10−11; normalized betweenness, β = −20.97; P = 8.79 × 10−4; eigenvector, β = −2.40; P = 5.12 × 10−3) (Fig. 4d and Supplementary Data 3). Gregarious people are less intimately related microbially to their social connections. This is apparent visually in Fig. 4e where participants are coloured based on their average strain-sharing rate with their first-degree connections.

Social clusters and microbiome clusters

The observed strain-sharing patterns along village, household, familial and social lines would mean that social clusters (that is, ‘communities’ of more densely interconnected people) should also have shared sets of particular microbiome species and strains. That is, the phenomena so far documented should come to instantiate or to reflect niches of microbiomes within niches of people (somewhat similar to soil biology33).

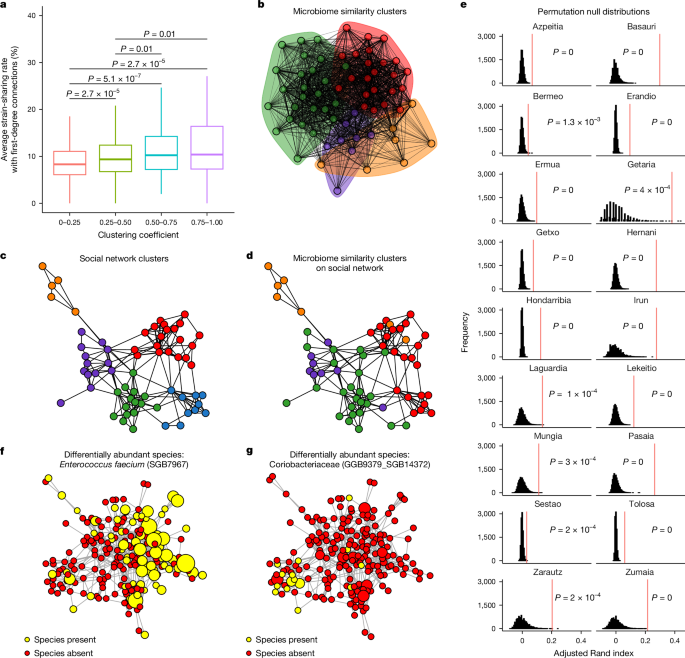
At the smallest scale, people with a higher clustering coefficient (that is, transitivity) are more likely to have a higher average strain-sharing rate to those connections (linear mixed-effects regression, β = 3.24; P = 7.32 × 10−7). Having relationships with people who are also connected to each other may promote microbiome circulation, leading to the formation of microbiome niches within social groups. Indeed, people with a high clustering coefficient (greater than or equal to 0.75) have a high average strain-sharing rate with their first-degree connections (median 10.3%). Conversely, people with a low clustering coefficient (less than or equal to 0.25) have a lower strain-sharing rate (8.43%) (two-sided Wilcoxon rank-sum test, Padj ≤ 0.05) (Fig. 5a).

Fig. 5: Social and microbiome strain niches.
figure 5

a, People with a higher clustering coefficient are, on average, more similar to their first-degree connections (n = 1,753; two-sided Wilcoxon rank-sum tests). Data are represented as boxplots where the middle line is the median and the lower and upper hinges correspond to the first and third quartiles. The whiskers extend from the hinge to the largest or smallest value no further than 1.5× IQR from the hinge. b, Microbiome strain-sharing-rate Louvain clusters for the village of Basauri. Ties are weighted and sized according to the strain-sharing rate between the pair of people (modularity = 0.18). c, Social network Louvain clusters for the village of Basauri (modularity = 0.58). d, Microbiome cluster membership painted onto the social network. There is visual overlap between communities detected solely on the basis of shared microbe sets and communities detected based solely on social connections. e, P value distributions for clustering results. Histograms represent the null distribution of adjusted Rand index values from 10,000 microbiome permutations. All villages are significant (permutation test for Azpeitia, Basauri, Erandio, Ermua, Getxo, Hernani, Hondarribia, Irun, Lekeitio, Pasaia, Tolosa and Zumaia, P = 0; Bermeo, P = 1.3 × 10−3; Getaria, P = 4 × 10−4; Laguardia, P = 1 × 10−4; Mungia, P = 3 × 10−4; Sestao, P = 2 × 10−4; Zarautz, P = 2 × 10−4), with the observed overlap metric represented by the vertical red line. f,g, Examples of two differentially abundant species, Enterococcus faecium (f) and SGB14372 (g), within the village of Hondarribia. Nodes are scaled according to the log relative abundance of the species, with yellow indicating presence of the species and red indicating absence.

Full size image

To observe this phenomenon at a village scale, we identify both social and microbiome clusters using Louvain clustering34,35,36. If strain-sharing rates are significantly elevated within social network clusters, we would expect a correspondence between social network clusters and clusters of microbially similar people. We formed microbiome clusters based on the strain-sharing network within a village, with ties between people discerned solely by virtue of the extent to which they share microbiome strains and weighted by the strain-sharing rate (Fig. 5b and Supplementary Table 4). In parallel, we formed social clusters based on familial and social connections (without weighting) (Fig. 5c). On average, this method yielded social clusters of 11 people with an average of 24 intra-cluster relationships, and microbiome clusters of 17 people with an average intra-cluster strain-sharing rate of 8.5%. We can then paint the microbiome cluster membership onto the social network clustering and visualize the correspondence between social communities and microbiome communities (Fig. 5d) (as a robustness check, we also evaluated Leiden clustering37; Supplementary Fig. 9).

Across the villages, social clusters overlap visually with microbiome clusters (shown for one village in Fig. 5b–d). To test this effect statistically, we can evaluate the correspondence between social and microbiome cluster membership with the adjusted Rand index38. To observe the distribution of this statistic if there was independence between the microbiome of a host and their social network, we can compare our observed index to a microbiome permutation null, where we randomly swap the microbiome of every person in the village. We observe that social cliques correspond to microbial cliques at a significant rate in all 18 villages (maximum P < 0.05) (Fig. 5e). Across 10,000 microbiome permutations, in only two villages does any random permutation ever lead to more overlap between social and microbiome clusters than the observed overlap (Sestao and Zarautz in Fig. 5e).

If social clustering reinforces within-cluster microbial sharing, we would also expect different social clusters to have differentially abundant bacteria. To test this, we compared whether the relative abundance of each species differed across social clusters. After Benjamini–Hochberg multiple testing correction, we found 138 examples of species that were differentially abundant in different network communities out of 17,278 tests (Extended Data Fig. 6 shows the P value distributions of the Kruskal–Wallis tests). Figure 5f,g shows examples of two species (Enterococcus faecium (SGB7967) and Coriobacteriaceae SGB14372) that are differentially abundant in different network regions of an illustrative village.

Discussion

Using detailed social network mapping and strain-level microbiome genomics in 18 isolated Honduras villages, we find a substantial correspondence between social structure and microbiome sharing beyond familial or household relationships. The amount of strain-sharing seems to be modulated according to the nature of the social relationships, even after accounting for other measured attributes (such as diet and medications). More intimate relationships share more strains, and strain-sharing rates increase monotonically based on the frequency with which a pair of people shares meals or free time together. The strain-sharing rate was the strongest predictor of social relationships, beyond socio-demographic features such as wealth, religion or education. Pairs of people who are connected within a village also come to share more strains over a 2-year follow-up than otherwise similar pairs of unconnected people. Furthermore, we observe significantly elevated strain-sharing levels out to a social horizon of two degrees of separation. Host network position, whether central or peripheral, moderates exposure to the microbial metacommunity within the villages such that more socially isolated people tend to be more microbially isolated as well. Overall, the intricate groundwork provided by the social network structure of human populations seems to provide a set of niches within which microbes can thrive or spread.

We are unable to distinguish direct transmission of strains from indirect transfer (for example, via unobserved social connections), nor can we infer the directionality of any potential transmission between two people sharing a strain. Although we control for factors such as diet, medication use and water source, and although we have longitudinal data for some analyses, it is not possible—with observational data alone—to fully distinguish shared environment from transmission. However, the genetic specificity of strains is consistent with transmission, especially in light of the human-host specificity of some transmitted species39,40. Strain-level resolution helps shed light on the idea that similar microbial species seen within members of the same household may be based not only on a modulation by similar environmental conditions or shared genetics, but also on spread between people. Our ability to also find strain-sharing among people who are not genetically related and do not reside in the same household, but who are known to interact, bolsters this conclusion.

A previous study of 287 people in five villages in Fiji documented strain-sharing between spouses, household members and a subset of other social interactions1. A study examining 7,646 people from 31 communities in 20 (mostly developed) countries also focused on kin and same-household ties4, and reported that the strain-sharing rate for the gut microbiome for non-cohabiting adults within the same village generally was 8%. Our estimate of this parameter was 4%. However, since we mapped a wider range of social relationships, beyond just familial or household ties, we have a clearer understanding of whether village co-residents actually interact with one another. In other words, our estimate of pairs of people who are simply village co-residents includes only people who do not, in fact, interact socially.

Using both observational and experimental methods, diverse phenomena have been shown to spread interpersonally, including phenotypes such as obesity and depression41,42. To the extent that the microbiome can be associated with physical or mental states43, then any spread of the microbiome via biological contagion may partly explain the ostensible spread of certain other attributes via social contagion41,44. It may prove to be the case that groups of interconnected people might share phenotypes not only because of shared genes or transmitted behaviours, but also because of shared microbes.

Methods

Local involvement and ethics

We worked closely with the local population of Copan, sought approval and feedback from officials at the Ministry of Health (MOH) of Honduras, and endeavoured to provide practical benefits to the local community. When we began designing the underlying cohort project in 2013 (in 176 villages, including the 18 used here), the Bill and Melinda Gates Foundation introduced us to the Inter-American Development Bank (IDB), which has been supporting and doing work throughout Latin America, and the IDB in turn introduced us to the MOH. Because of this pathway to getting the project launched, we worked with local and regional public health agencies and with local leaders rather than with academic partners.

The area we chose to work in the western highlands of Honduras, Copan, is very isolated. Over the years, as we built our data collection team in Copan, we developed deep ties to the local community, to local village leaders and to the few local health clinics there, as well as to local transportation and infrastructure providers. Because of these ties and our commitment to the local community, we presented our results directly to these constituencies regularly at the completion of our various projects.

We provided other material benefits to the local community, beyond simply providing them with information. When we tested people for stool parasites, we gave them the results of their tests and arranged for them to be treated. When we tested people for vision, we provided corrective glasses. We solicited ideas from the local community about what infrastructure improvements we could make, and we repaired many local playgrounds and clinics as a result. We arranged for an American company to provide free portable handheld ultrasound devices to the local health clinics, which was much appreciated by local providers. In terms of capacity building, we hired and trained over 100 local people, and many of our former data collectors have gone on to work for other public health and development entities. Finally, we offered a talented young person from Copan a position as a PhD student in the USA.

Throughout our work in Honduras, along with our extensive involvement at local and national levels, we have endeavoured to act with integrity, curiosity and respect in all our relationships.

This research would not have been prohibited in the USA. This work is not likely to result in stigmatization, incrimination or discrimination or personal risk for the participants, and we have safeguarded all data from threats to the privacy or security of our participants.

All participants provided informed consent, and our work was approved by the Yale Committee on Human Subjects (reference no. 2000020688).

Network construction

Village-level networks were mapped with standard ‘name generators’ for the whole village. After a photographic census (of all adolescent and adult residents) was taken for each village, we conducted the main network survey in each village, including a detailed, hour-long survey7, incorporating demographic and health measures, as well as a battery of name generators with which respondents identified relevant social relationships (friends, family members, people they spend free time with, and so on) through names and photographs shown in our TRELLIS software (available at trellis.yale.edu)45. All the name generator questions are listed in Supplementary Table 1.

For questions in which a pair reported different levels of the same variable, such as greeting type or the amount of free time, we symmetrized the variables as follows: for greeting type, we reported the greeting type involving the most physical contact. For the frequency of free time and shared meals between a pair, we symmetrized by choosing the response that indicates more frequent contact. We symmetrized all other responses at the relationship level here (that is, when either of two people nominate each other as a ‘close friend’, we counted it). When calculating degree distributions, centralities and clustering, we simplified our networks to remove multiplexity (that is, we concatenated all ties between pairs of people) and symmetrized the ties (that is, we ignored who nominated whom in each pair).

Social network graphs were analysed and geodesic distances and centrality measures were calculated with igraph (v.1.3.5)46 and plotted with the Fruchterman–Reingold algorithm. To protect the anonymity of our study villages, the villages were renamed to random town names from another country.

Sample collection and sequencing

Participants were instructed on how to self-collect the faecal samples using a training module delivered in person in the villages and were asked to return samples promptly to the local team. Samples were refrigerated immediately upon collection and then stored in liquid nitrogen at the collection site within 12 h after collection and moved to a −80 °C freezer in Copan Ruinas, Honduras. All the villages followed the same procedures. Samples were shipped, in randomized allotments, on dry ice to the USA and stored in −80 °C freezers.

Stool material was homogenized using TissueLyzer from Qiagen, and the lysate was prepared for extraction with the Chemagic Stool gDNA extraction kit (Perkin Elmer) and extracted on the Chemagic 360 Instrument (Perkin Elmer) following the manufacturer’s protocol. Sequencing libraries were prepared using the KAPA Hyper Library Preparation kit (KAPA Biosystems). Shotgun metagenomic sequencing was carried out on Illumina NovaSeq 6000. Samples not reaching the desired sequencing depth of 50 Gbp were resequenced on a separate run. Raw metagenomic reads were deduplicated using prinseq lite47 (v.0.20.2) with default parameters. The resulting reads were screened for human contamination (hg19) with BMTagger and then quality filtered with Trimmomatic48 (v.0.36, parameters ‘ILLUMINACLIP: nextera_truseq_adapters.fasta:2:30:10:8:true SLIDINGWINDOW: 4:15 LEADING: 3 TRAILING: 3 MINLEN: 50’). This resulted in a total of 1,787 samples (with an average size of 8.6 × 107 reads).

Species-level and strain-level profiling

Species-level profiling was performed using MetaPhlAn 426 using the Jan21 database and default parameters. Strain-level profiling was performed for a subset of species present in at least 50 samples using StrainPhlAn 426 with parameters ‘–marker_in_n_samples 1 –sample_with_n_markers 10 — phylophlan_mode accurate’. This resulted in a total of 841 species-level genome bins (SGB) and 339,137 profiled strains. The StrainPhlAn ‘strain_transmission.py’ script was used to assess transmission events using the produced trees, which yielded a total of 513,177 identified events. For a robust calculation, strain-sharing rates were calculated only for pairs sharing at least ten SGBs.

Beta diversity indices were calculated using the vegdist function from the vegan R package (v.2.6-2)49.

Separation of distances by village membership was tested by permutational multivariate analysis of variance (PERMANOVA) using the adonis function from the vegan R package with 999 permutations.

Statistical analyses

All statistical analyses were performed in R (v.4.1.3). Correction for multiple testing (Benjamini–Hochberg procedure, marked Padj) was applied when appropriate, and significance was defined at Padj< 0.05. All tests were two-sided except where otherwise specified. All egocentric regressions (that is, when we assess the relationship of network position and strain-sharing) involved linear mixed-effects models with this general formula specification:

$$begin{array}{c}{rm{O}}{rm{u}}{rm{t}}{rm{c}}{rm{o}}{rm{m}}{rm{e}},{rm{o}}{rm{f}},{rm{i}}{rm{n}}{rm{t}}{rm{e}}{rm{r}}{rm{e}}{rm{s}}{rm{t}} sim {rm{p}}{rm{r}}{rm{e}}{rm{d}}{rm{i}}{rm{c}}{rm{t}}{rm{o}}{rm{r}},{rm{o}}{rm{f}},{rm{i}}{rm{n}}{rm{t}}{rm{e}}{rm{r}}{rm{e}}{rm{s}}{rm{t}}+{rm{a}}{rm{g}}{rm{e}}+{rm{s}}{rm{e}}{rm{x}} ,+,{rm{B}}{rm{M}}{rm{I}}+{rm{B}}{rm{r}}{rm{i}}{rm{s}}{rm{t}}{rm{o}}{rm{l}},{rm{s}}{rm{t}}{rm{o}}{rm{o}}{rm{l}},{rm{s}}{rm{c}}{rm{a}}{rm{l}}{rm{e}}+{rm{h}}{rm{o}}{rm{u}}{rm{s}}{rm{e}}{rm{h}}{rm{o}}{rm{l}}{rm{d}},{rm{w}}{rm{e}}{rm{a}}{rm{l}}{rm{t}}{rm{h}},{rm{i}}{rm{n}}{rm{d}}{rm{e}}{rm{x}} ,+,{rm{d}}{rm{i}}{rm{e}}{rm{t}},{rm{d}}{rm{i}}{rm{v}}{rm{e}}{rm{r}}{rm{s}}{rm{i}}{rm{t}}{rm{y}},{rm{s}}{rm{c}}{rm{o}}{rm{r}}{rm{e}}+{rm{m}}{rm{e}}{rm{d}}{rm{i}}{rm{c}}{rm{a}}{rm{t}}{rm{i}}{rm{o}}{rm{n}},{rm{u}}{rm{s}}{rm{a}}{rm{g}}{rm{e}}+{rm{w}}{rm{a}}{rm{t}}{rm{e}}{rm{r}},{rm{s}}{rm{o}}{rm{u}}{rm{r}}{rm{c}}{rm{e}} ,+,{rm{D}}{rm{N}}{rm{A}},{rm{c}}{rm{o}}{rm{n}}{rm{c}}{rm{e}}{rm{n}}{rm{t}}{rm{r}}{rm{a}}{rm{t}}{rm{i}}{rm{o}}{rm{n}}+{rm{s}}{rm{e}}{rm{q}}{rm{u}}{rm{e}}{rm{n}}{rm{c}}{rm{i}}{rm{n}}{rm{g}},{rm{d}}{rm{e}}{rm{p}}{rm{t}}{rm{h}}+{rm{e}}{rm{x}}{rm{t}}{rm{r}}{rm{a}}{rm{c}}{rm{t}}{rm{i}}{rm{o}}{rm{n}},{rm{d}}{rm{a}}{rm{t}}{rm{e}} ,+,{rm{s}}{rm{h}}{rm{i}}{rm{p}}{rm{p}}{rm{i}}{rm{n}}{rm{g}},{rm{b}}{rm{a}}{rm{t}}{rm{c}}{rm{h}}+{rm{s}}{rm{e}}{rm{q}}{rm{u}}{rm{e}}{rm{n}}{rm{c}}{rm{i}}{rm{n}}{rm{g}},{rm{b}}{rm{a}}{rm{t}}{rm{c}}{rm{h}}+{rm{e}}{rm{x}}{rm{t}}{rm{r}}{rm{a}}{rm{c}}{rm{t}}{rm{i}}{rm{o}}{rm{n}},{rm{b}}{rm{a}}{rm{t}}{rm{c}}{rm{h}} ,+,(1|{rm{v}}{rm{i}}{rm{l}}{rm{l}}{rm{a}}{rm{g}}{rm{e}})+(1|{rm{b}}{rm{u}}{rm{i}}{rm{l}}{rm{d}}{rm{i}}{rm{n}}{rm{g}})end{array}$$

That is, we controlled for age, sex, wealth, Bristol stool scale and body mass index (BMI), as well as sample properties (for example, DNA concentration) and village fixed effects. We also included household water source, individual medication usage in the last month and diet diversity (the number of food categories consumed on a daily basis10). Medication types included: painkillers, antibiotics, anti-diarrhoeal, anti-parasitic, anti-fungal, anti-diabetics, antacids, laxatives and vitamins. Mixed-effects models were created with the lmertest package (v.3.1.3)50.

Network predictions

Mixed-effects logistic regression models were used for out-of-sample network predictions. Class-balanced data sets were constructed by down-sampling the number of unrelated pairs to equal the number of related pairs, and we trained our model using k-fold cross-validation with k = 3, and predictions from the three separate test sets were combined. ROC curves were constructed from the average of five sets of threefold cross-validation. ROC curves and confidence intervals were calculated with the pROC package (v.1.18.0)51 and logistic regression models were constructed with the lmertest package (v.3.1.3) with the binomial family link function and a random slope per village.

The predictive model including all covariates was specified by the following formula:

$$begin{array}{c}{rm{R}}{rm{e}}{rm{l}}{rm{a}}{rm{t}}{rm{i}}{rm{o}}{rm{n}}{rm{s}}{rm{h}}{rm{i}}{rm{p}} sim {rm{m}}{rm{i}}{rm{c}}{rm{r}}{rm{o}}{rm{b}}{rm{i}}{rm{o}}{rm{m}}{rm{e}},{rm{s}}{rm{i}}{rm{m}}{rm{i}}{rm{l}}{rm{a}}{rm{r}}{rm{i}}{rm{t}}{rm{y}}+{rm{s}}{rm{e}}{rm{x}} ,+,{rm{i}}{rm{n}}{rm{d}}{rm{i}}{rm{g}}{rm{e}}{rm{n}}{rm{o}}{rm{u}}{rm{s}},{rm{s}}{rm{t}}{rm{a}}{rm{t}}{rm{u}}{rm{s}}+{rm{r}}{rm{e}}{rm{l}}{rm{i}}{rm{g}}{rm{i}}{rm{o}}{rm{n}}+{rm{a}}{rm{g}}{rm{e}},{rm{d}}{rm{i}}{rm{f}}{rm{f}}{rm{e}}{rm{r}}{rm{e}}{rm{n}}{rm{c}}{rm{e}} ,+,{rm{a}}{rm{v}}{rm{e}}{rm{r}}{rm{a}}{rm{g}}{rm{e}},{rm{a}}{rm{g}}{rm{e}}+{rm{w}}{rm{e}}{rm{a}}{rm{l}}{rm{t}}{rm{h}},{rm{d}}{rm{i}}{rm{f}}{rm{f}}{rm{e}}{rm{r}}{rm{e}}{rm{n}}{rm{c}}{rm{e}}+{rm{a}}{rm{v}}{rm{e}}{rm{r}}{rm{a}}{rm{g}}{rm{e}},{rm{w}}{rm{e}}{rm{a}}{rm{l}}{rm{t}}{rm{h}} ,+,{rm{e}}{rm{d}}{rm{u}}{rm{c}}{rm{a}}{rm{t}}{rm{i}}{rm{o}}{rm{n}},{rm{d}}{rm{i}}{rm{f}}{rm{f}}{rm{e}}{rm{r}}{rm{e}}{rm{n}}{rm{c}}{rm{e}}+{rm{a}}{rm{v}}{rm{e}}{rm{r}}{rm{a}}{rm{g}}{rm{e}},{rm{e}}{rm{d}}{rm{u}}{rm{c}}{rm{a}}{rm{t}}{rm{i}}{rm{o}}{rm{n}} ,+,{rm{m}}{rm{e}}{rm{d}}{rm{i}}{rm{c}}{rm{a}}{rm{t}}{rm{i}}{rm{o}}{rm{n}},{rm{u}}{rm{s}}{rm{a}}{rm{g}}{rm{e}}+{rm{s}}{rm{a}}{rm{m}}{rm{e}},{rm{w}}{rm{a}}{rm{t}}{rm{e}}{rm{r}},{rm{s}}{rm{o}}{rm{u}}{rm{r}}{rm{c}}{rm{e}}+{rm{d}}{rm{i}}{rm{e}}{rm{t}} ,+,{rm{B}}{rm{r}}{rm{i}}{rm{s}}{rm{t}}{rm{o}}{rm{l}},{rm{s}}{rm{t}}{rm{o}}{rm{o}}{rm{l}},{rm{s}}{rm{c}}{rm{a}}{rm{l}}{rm{e}}+{rm{h}}{rm{o}}{rm{u}}{rm{s}}{rm{e}}{rm{h}}{rm{o}}{rm{l}}{rm{d}},{rm{s}}{rm{h}}{rm{a}}{rm{r}}{rm{i}}{rm{n}}{rm{g}} ,+,(0+{rm{m}}{rm{i}}{rm{c}}{rm{r}}{rm{o}}{rm{b}}{rm{i}}{rm{o}}{rm{m}}{rm{e}},{rm{s}}{rm{i}}{rm{m}}{rm{i}}{rm{l}}{rm{a}}{rm{r}}{rm{i}}{rm{t}}{rm{y}}|{rm{v}}{rm{i}}{rm{l}}{rm{l}}{rm{a}}{rm{g}}{rm{e}},{rm{I}}{rm{D}})end{array}$$

where ‘microbiome similarity’ is either the strain-sharing rate, Jaccard index or Bray–Curtis dissimilarity calculated between the members of a pair.

Variable importance metrics were calculated based on the permutation feature importance metric using the car R package (v.3.0). The permutation feature importance is defined to be the decrease in a model score when a single feature value is shuffled randomly52. This procedure breaks the relationship between the feature and the target; thus, the drop in the model score is indicative of how much the model depends on the feature. Variable importance metrics were analysed after 1,000 random permutations of each feature. Variable inflation factor values were calculated to ensure the reliability of results against collinearity of variables and were all low (less than 2).

Microbiome null permutations

Microbiome null permutations create a null distribution of strain-sharing rates between any two people while accounting for (just) the network structure. Under the null hypothesis that a host’s microbiome composition and social network are independent, we can sever their relationship by randomly permuting the microbiome of every person in the village and recalculating metrics of interest, for example, strain-sharing by degree or clustering Rand indices. This ensures that the inherent structural pattern of the network remains the same, but the node values are randomized. This allows us to observe the distribution of our statistics if the human microbiome is fostered independently of any host social interactions.

Village-wide microbiome permutations were used to calculate null distributions for the strain-sharing rate by geodesic distance and for the clustering results. For relationship-specific permutations in Supplementary Fig. 1, permutations at the relationship level were taken instead of full village permutations. The observed distribution of relationship-specific sharing was compared with the distribution of sharing observed when that specific relationship tie was permuted, for example, comparing the sharing between someone and their friend versus someone and 100 random people’s friends in the same village. For the inherently gendered relationships of husband/wife and mother/father of a child, we accounted for the sex of the ego, but for all other relationships that are not necessarily gendered (for example, free time), we did not.

Longitudinal analyses

A subset of 301 people from four villages were followed-up after a period of 2 years and asked to provide a second stool sample. Samples were processed consistently with the same pipeline used to analyse the previously processed 1,787 samples.

We defined relationship ties by using the same social network from the initial wave and evaluated the following linear mixed-effect model formula:

$${rm{SS}}{{rm{R}}}_{{rm{T}}2} sim SS{R}_{{rm{T}}1}+{rm{relationship}}+M+(1| {rm{village}},{rm{ID}})+(1| {rm{ego}})$$

where SSRT1 and SSRT2 are the strain-sharing rate in pairs of people at time points T1 and T2, respectively. We show standardized coefficients.

To decompose the effect of sharing across all species, we used a mixed-effect logistic model formula specified as follows:

$${rm{T}}{2}_{S} sim {rm{T}}{1}_{S}+{rm{relationship}}+M+(1| {rm{species}})+(1| {rm{villageID}})+(1| {rm{ego}})$$

where ({rm{T}}{1}_{S}) and ({rm{T}}{2}_{S}) are binary variables indicating whether we observed strain-sharing of an individual species at time point T1 or T2, for all species combined. A random intercept for each individual species was added as well as for village membership and person.

In both models, ‘relationship’ is a dummy variable indicating the presence (or absence) of a tie between the pair of people, and M is the Mahalanobis distance calculated on the following covariates:

$$begin{array}{c}M={rm{M}}{rm{a}}{rm{h}}{rm{a}}{rm{l}}{rm{a}}{rm{n}}{rm{o}}{rm{b}}{rm{i}}{rm{s}}({rm{a}}{rm{g}}{rm{e}},{rm{s}}{rm{e}}{rm{x}},{rm{B}}{rm{M}}{rm{I}},{rm{B}}{rm{r}}{rm{i}}{rm{s}}{rm{t}}{rm{o}}{rm{l}},{rm{s}}{rm{t}}{rm{o}}{rm{o}}{rm{l}},{rm{s}}{rm{c}}{rm{a}}{rm{l}}{rm{e}}, ,,{rm{h}}{rm{o}}{rm{u}}{rm{s}}{rm{e}}{rm{h}}{rm{o}}{rm{l}}{rm{d}},{rm{w}}{rm{e}}{rm{a}}{rm{l}}{rm{t}}{rm{h}},{rm{i}}{rm{n}}{rm{d}}{rm{e}}{rm{x}},{rm{d}}{rm{i}}{rm{e}}{rm{t}},{rm{d}}{rm{i}}{rm{v}}{rm{e}}{rm{r}}{rm{s}}{rm{i}}{rm{t}}{rm{y}},{rm{i}}{rm{n}}{rm{d}}{rm{e}}{rm{x}}, ,,{rm{m}}{rm{e}}{rm{d}}{rm{i}}{rm{c}}{rm{a}}{rm{t}}{rm{i}}{rm{o}}{rm{n}},{rm{u}}{rm{s}}{rm{a}}{rm{g}}{rm{e}},{rm{w}}{rm{a}}{rm{t}}{rm{e}}{rm{r}},{rm{s}}{rm{o}}{rm{u}}{rm{r}}{rm{c}}{rm{e}},{rm{b}}{rm{u}}{rm{i}}{rm{l}}{rm{d}}{rm{i}}{rm{n}}{rm{g}},{rm{I}}{rm{D}})end{array}$$

The pairwise Mahalanobis distance was calculated on the covariates matrix using the D2.dist function from the biotools R package53 (v.4.2). We also specified this model using the constituent variables, rather than the Mahalonobis distance (Supplementary Data 2).

Microbiome and social clustering

We use the Louvain and the Leiden methods as implemented in the igraph package to cluster participants along social and microbiome lines. Louvain clustering is based on greedy modularity optimization. Modularity is a scale value between −0.5 (non-modular clustering) and 1 (fully modular clustering) that measures the relative density of edges inside communities compared with edges outside communities. Optimizing this value theoretically results in the best possible grouping of the nodes of a given network. In cases where a pair shared too few SGBs to calculate a robust strain-sharing rate (fewer than ten), a strain-sharing rate of 0% was imputed to allow for proper weight-based clustering. This occurred in 0.45% of the pairwise comparisons (16,228 out of 3,560,769 comparisons), and just 838 of the 16,228 comparisons were from people in the same village. The adjusted Rand index was calculated with the mclust package (v.6.0.0)54.

For testing species differential abundance across network communities with the Kruskal–Wallis test, robustness checks ensuring that each social cluster had more than five people and the species was present in more than five people in the village were performed, and cases where this criterion was not met were excluded.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.