Introduction

In the modern era of fast, global information flows, beyond the spread of innovations1,2 or opinions3,4,5, information wars and infodemics6,7 present a scenario where individuals and algorithms with different adoption or learning profiles co-exist and spread information in complex networks. Intentionally, organizations can influence and sponsor individuals to propagate specific opinions, news, or facts, aiming at turning information viral and shaping public perceptions and views about varied topics8. Indeed, organizations have used bot farms9,10,11 or cyber armies12 embedded in the fabric of social media platforms, which are often indistinguishable from normal users13, to amplify the propagation of information or to keep platforms active. Network segregation has experimentally shown to favor the diffusion of false news14. The effectiveness of such interventions underscores the importance of understanding the underlying dynamics of information diffusion on heterogeneous social networks and, particularly, the different roles individuals play.

A core assumption in past works is that the type of information being spread defines the type of adoption/learning process15,16. Consequently, it is tradition to consider homogeneous populations regarding individuals’ learning profiles and spreading behaviors. For instance, individuals learn through contact (simple contagion17,18,19,20,21,22) or social pressure (complex contagion3,23,24,25,26,27,28,29). Naturally, all these models overlap in specific limits30 or interpretations and have their merits for addressing specific research questions, as they extend our understanding of the spread of different types of information—e.g., opinions, innovations, political affiliation, behaviors, habits—that we know to leave different distinguishable empirical traces31,32,33,34, and that may have different intervention points.

However, such an assumption of homogeneity can be insufficient35,36. Indeed, in human-algorithm mixes, responses are expected to differ (i.e., between bots and humans). Even among humans, individuals with many friends/followers might not find it efficient to learn through simple imitation and, instead, rely on a general perception of the prevalence of opinions in their neighborhood to make decisions involving adopting new technology or behavior3,27. In contrast, agents aiming to transmit specific information will share it as soon as they see it. From another viewpoint, some individuals might be more eager to adopt innovations in their neighborhood while others are more adverse to change and require pressure from multiple friends to adopt it37,38,39.

Several studies have examined how individuals with varying susceptibility or influence can impede or facilitate diffusion processes. For instance, threshold-based agents have been explored primarily under homogeneous assumptions–focusing on either structural or behavioral effects in isolation40,41. Further, most prior work considers static or random distributions of agent types, overlooking the strategic placement of different learner profiles within degree-heterogeneous networks. Recent advances suggest that network topology interacts strongly with node-level behaviors42, highlighting the need to investigate how high-degree nodes adopting stricter thresholds alter global diffusion patterns43. And in the context of influence maximization literature much effort has been put into identifying best seeding strategies that maximize the unfolding cascades23,44,45,46,47,48

Given these examples, a more reasonable assumption is that populations are heterogeneous and contain individuals with different learning/adoption preferences/profiles36,41. Such a co-existence of learning preferences creates rich dynamics in the irreversible adoption of information, including continuous and discontinuous phase transitions as the contact probability increases49.

Here, we consider the case of a heterogeneous population of Simple Spreaders (individuals that activate through contact, i.e., simple contagion) and Threshold-based Spreaders (whose adoption of information requires reinforcement from multiple peers, which we implement through a threshold function of the percentage of friends sharing the information, i.e., complex contagion). In that context, Simple Spreaders can be seen as individuals in the social fabric that promote the views of an external organization9,50,51. We extend the literature by focusing on how the strategic placement of adoption profiles in different networks can regulate the spread of information. Understanding the strategic placement of agents can provide valuable insights into the effectiveness of information diffusion strategies, particularly in the context of information warfare.

Starting from a few seeds (i.e., the initial spreaders) placed randomly in the population, we explore how the size of an information cascade depends on the balance of Simple and Threshold-based Spreaders for different arrangements of these roles on social networks. We show that while scale-free networks facilitate larger cascade sizes for randomly placed roles in the population, they create obstacles when Threshold-based Spreaders preferentially occupy the network’s most well-connected elements, meaning that cascades require many Simple Spreaders to unfold, an effect that is amplified on disassortative networks. Our results remain qualitatively consistent for increasing number of seeding nodes, suggesting a robust dynamical outcome and the role of Threshold-based spreaders as information filters.

Model & methods

Social structure

Let us consider a population of Z individuals whose social interactions are represented through a complex network. Individuals occupy the network nodes, while edges connect pairs of individuals and indicate the presence of a mutual social relationship of influence. As such, information spreads through social ties, i.e., the edges of the social network. The number of relationships an individual participates in defines their degree (k_i), and D(k) is the degree distribution that describes the relative frequency of individuals with degree k. The average degree of the population is (langle k rangle = sum _k k D(k)), which we fix across network types.

We consider three types of complex networks—Random (ER), Exponential (Exp), and Scale-Free (SFBA)—as the baseline structures. Random networks are generated using the Erdös–Rényi model52, Scale-Free networks using the Barabási–Albert algorithm53 of growth and preferential attachment, and Exponential networks are generated following the growth algorithm of Barabási-Albert but with random attachment. These three networks provide three structures with low (ER), middle (Exp), and high (SFBA) levels of degree heterogeneity as measured by the variance of the degree distribution54.

To generate degree Assortative and Disassortative variants of Scale-Free networks (SFBA)55, we implement the Xulvi-Brunet56 algorithm with the constrain that only rewires that do not disconnect the network are accepted.

Finally, we generate a set of scale-free networks with different exponents through an algorithm that combines network growth with biased preferential attachment57,58,59 that proceeds as follows: starting from a clique of three nodes, (Z-3) other nodes are added sequentially; each of the newly added nodes attaches to two pre-existing (resulting in a network with average degree of four) ones sampled proportionally to (t^{-alpha }) ((0.0 le alpha le 1.0)) where t corresponds to the ranked age of the nodes and (alpha) is a control parameter. The generated networks exhibit a power law degree distribution of the form (D(k) approx k^{-gamma }), which in the limiting case of (Z rightarrow infty) is defined by the control parameter (alpha) as (gamma = (1 + alpha )/alpha)57,58.

More importantly, and besides the relationship with (gamma), a more interesting interpretation of (alpha) is that it regulates the level of degree heterogeneity of the resulting networks as it exhibits both a one-to-one relationship with (gamma) and var(k), so that a low (large) (alpha) is associated with a low (large) level of degree heterogeneity. We generate eleven sets of such networks within the range of (alpha = 1/3) to (alpha = 1.0) that exhibit exponents ranging between (gamma approx 3.30) and (gamma approx 2.25), respectively. The variance of the degree distribution of the highest degree heterogeneous network ((alpha = 1.0) and (gamma = 2.25)) is 15 times larger than that of the least heterogeneous one ((alpha = 1.0) and (gamma = 2.25)).

To account for the stochasticity of the network generation models, we independently generated 100 instances of each network type.

Cascade dynamics

Individuals can be in one of two states: active or inactive. Active means that they have already adopted the information being spread and can also spread it. Inactive means that individuals have the potential to adopt the information and are not able to spread it or influence their peers. We consider two types of individuals that characterize their update rule, or Learning Profile, when inactive: Simple Spreaders and Threshold-based Spreaders. (Inactive) Simple Spreaders copy the state of a random neighbor. (Inactive) Threshold-based Spreaders become active if the fraction of active neighbors is above (Gamma).

At the start of each simulation, we consider every individual except for a small number of seeds inactive. Hence, the seeds correspond to a subset of active individuals that are responsible for the start of the spreading of (novel) information in the population. We consider seeds placed randomly in the population.

In contrast with past works40,60, we assume individuals can update their state differently. In that sense, a fraction (theta) of individuals adopt a new state through pure imitation of random neighbors (i.e., simple contagion), Simple Spreaders. While the remaining fraction of individuals, (1-theta), requires reinforcement from multiple friends (i.e., complex contagion) to change their state, Threshold-based Spreaders.

Fig. 1
figure 1

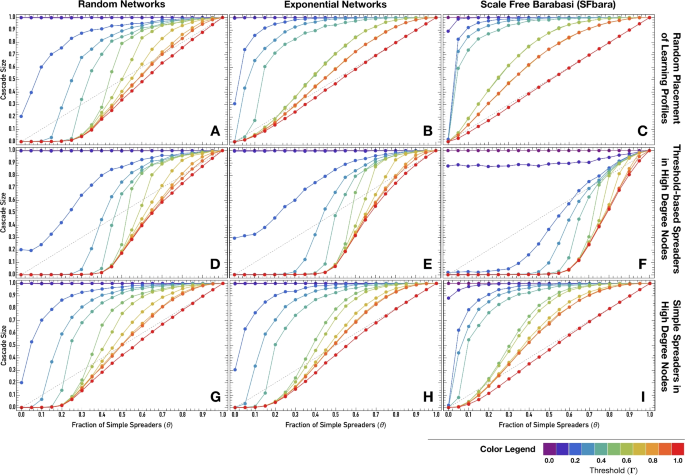
Cascade sizes with one seeding individual when learning profiles are placed at random (A–C) and when threshold-based (D–F) or simple (G–I) spreaders are placed preferentially in high degree nodes. The diagonal dashed line represents the identity in which an increase in the fraction of Simple Spreaders ((theta)) would lead to an equal increase in the final fraction of activated individuals (cascade size). Colors indicate different levels of the threshold used for threshold-based spreaders ((Gamma)): 0.0 (purple), 0.50 (green), and 1.00 (red). Other parameters are (Z = 10^3) and (langle k rangle = 4). For each condition, the reported results represent the average over 1000 simulations for each of the 100 network instances, totaling (10^5) independent simulations.

Full size image

We model the spreading dynamics as an asynchronous process in which, at each iteration, a random individual i is selected to potentially update its state from inactive to active. If i is already active, we skip to the next iteration, irrespective of the type. If i is inactive and a Simple Spreader, then i will sample a random neighbor j and copy its state. This means that if j is active, i also becomes active; otherwise, it remains inactive. Finally, if i is inactive and a Threshold-based Spreader, then i will evaluate the fraction of active neighbors ((gamma _i)), and, if (gamma _i > Gamma), i will become active. At each time step, there are n active individuals and (Z-n) inactive individuals in the population.

In each simulation, we repeat the update steps until the simulation either reaches (i) a maximum of (Ztimes 10^6) iterations, (ii) the population reaches a monomorphic configuration where all individuals are active, or (iii) the number of active individuals remains the same for (Z times 10^2) iterations. The final fraction of active individuals ((x = n/Z)) corresponds to the cascade size, which we average over (10^5) independent simulations.

Results

Analytical insights

To gain some intuition on this process, we consider the theory of percolation in infinite graphs. Our cascades can be analyzed in two distinct stages: the percolation of simple spreaders (SS) and the subsequent activation of threshold-based spreaders (TBS). This sequential analysis is rational because TBS will not activate spontaneously, and the formation of a giant connected component of SS serves as the backbone for triggering TBS activation through a bootstrap process. The general condition for percolation of SS nodes is that their average excess degree exceeds 1.

In Erdös–Rényi (ER) networks, this requires the fraction of SS-nodes, (theta), to be greater than (1/langle krangle), where (langle krangle) is the average degree of the network. Additionally, using a coarse mean-field approximation that assumes a homogenous degree, (theta) must exceed the threshold (Gamma) of TBS to ensure their activation, creating an additional constraint in (theta).

Due to the high degree of heterogeneity in scale-free networks, we rely on heterogeneous mean-field approximations to describe the activation dynamics. The Mollow-Reed percolation condition still holds in its general form (frac{langle k(k-1)theta rangle }{langle k theta rangle }>1). When individuals are equally distributed across degrees, the fraction of SS-nodes per degree is (theta =theta) for all degrees. Thus, it becomes clear that the percolation of SS-nodes depends on the degree-distribution exponent (gamma): for (gamma le 3), the numerator diverges, and the presence of hubs ensures that SS-nodes percolate even at very small (theta), while for (gamma >3), the condition requires a positive (theta).

The condition for the percolation of TBSs following that of SSs requires numerical analysis. Degree-dependent assignment of a proportion (theta _k) of SS in a degree-k class significantly influences the minimal fraction of SSs required for both SS- and TBS-node activation. A clear example is using a power-law relation for distributing SSs along degree, (theta _k ~ k^{-eta }), where higher (eta) places more TBSs in higher degree nodes. Then, high enough (eta) can regularize the sum even for (gamma le 3), preventing percolation of SSs for small fractions of SSs as long as (eta >gamma -3). In what follows, we explore the cascade size systematically using simulation.

To gain some intuition on this process, we consider the theory of percolation in infinite graphs. Our cascades can be analyzed in two distinct stages: the percolation of Simple Spreaders (SS) and the subsequent activation of Threshold-based Spreaders (TBS). This sequential analysis is rational because TBS will not activate spontaneously, and the formation of a giant connected component of SS serves as the backbone for triggering TBS activation through a bootstrap process. The general condition for percolation of SS nodes is that their average excess degree exceeds 161.

In Erdös–Rényi (ER) networks, the first percolation of SS requires the fraction of SS-nodes, (theta), to be greater than (1/langle krangle), where (langle krangle) is the average degree of the network. Additionally, using a coarse mean-field approximation that assumes a homogenous degree, (theta) must exceed the threshold (Gamma) of TBS to ensure the activation of TBS, creating an additional constraint in (theta).

As for scale-free networks, we rely on heterogeneous mean-field approximations to describe the activation dynamics due to their high degree of heterogeneity. The Mollow-Reed percolation condition still holds in its general form (langle k(k-1)theta rangle / langle k theta rangle >1), where each class k is characterized by a fraction of SS nodes (alpha _k). When individuals are equally distributed across degrees, the fraction of SS nodes per degree is (theta _k = theta) for all degrees. Thus, it becomes clear that the percolation of SS nodes depends on the degree-distribution exponent (gamma): for (gamma le 3), the numerator diverges, and the presence of hubs ensures that SS nodes percolate even at very small (theta), while for (gamma >3), the condition requires a positive (theta). The condition for the percolation of TBSs following that of SSs requires numerical analysis. Degree-dependent assignments of a proportion (theta _k) of SS in a degree-k class significantly influence the minimal fraction of SSs required for both SS- and TBS-node activation. A clear example is using a power-law relation for distributing SSs along degree, (theta _k sim k^{-eta }), where higher (eta) places more TBSs in higher degree nodes (in the simulations that follow, we set (eta =1)). Then, high enough (eta) can regularize the sum even for (gamma le 3), preventing percolation of SSs for small fractions of SSs as long as (eta >gamma -3). In what follows, we explore the cascade size systematically using simulations.

Fig. 2
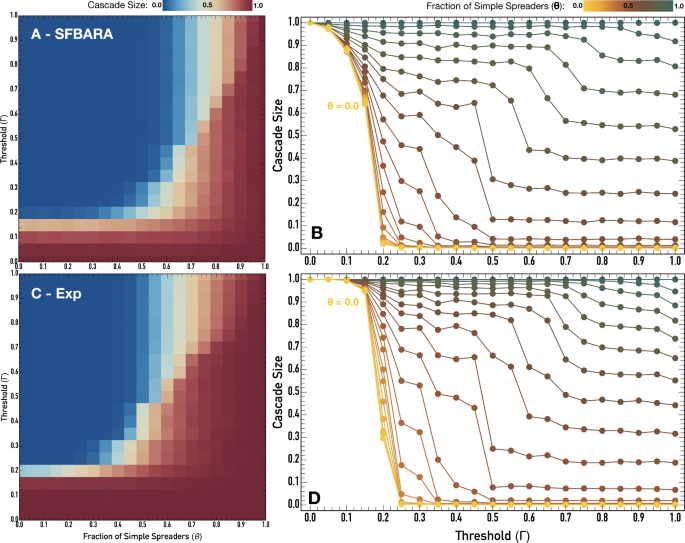
figure 2

Threshold-based Spreaders in high degree nodes. Cascade size as a function of threshold-based spreader threshold ((Gamma)) and the fraction of simple spreaders ((theta)). (A,C) The full picture with colors indicating no cascade (blue) or full cascade (red) parameter regions. (B,D) Cross-sections for different values of the fraction of simple spreaders ((theta)) with different colors. Other parameters are (Z = 10^3) and (langle k rangle = 4). For each condition, the reported results represent the average over 1000 simulations for each of the 100 network instances, totaling (10^5) independent simulations.

Full size image

Simulations

We start by considering a population composed by a fraction (theta) of Simple Spreaders and (1-theta) of Threshold-based Spreaders placed at random on the nodes of a network, and we simulate a cascade dynamics starting from a single randomly placed seed. We consider different thresholds ((Gamma)) for Threshold-based Spreaders—0.0 (purple), 0.25 (blue), 0.50 (green), 0.75 (yellow), and 1.00 (red)—and study the impact on different network structures: Random (A), Exponential (B), Scale-Free (C).

The two trivial limiting scenarios that easily verify the conditions for percolation are (Gamma = 0) (when Threshold-based Spreaders require only one active neighbor to become active) and (Gamma = 1) (when Threshold-based Spreaders never become active). Therefore, when (Gamma = 0), results are independent of (theta) (fraction of Simple Spreaders) and lead to the activation of the entire network network. In contrast, when (Gamma = 1), the identity line (dashed line) constitutes an upper bound of the cascade size. The cascades can be only as large as the proportion of Simple Spreaders ((theta)) in the population since Threshold-based Spreaders never update their state. However, Threshold-Based Spreaders may disconnect the SS and not allow for a complete cascade for a low enough average degree.

Fig. 3
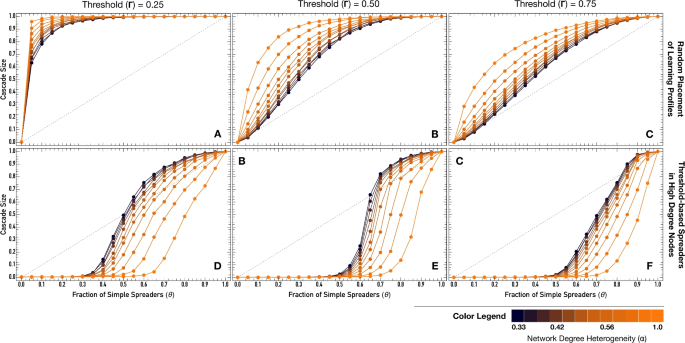
figure 3

Effect of degree heterogeneity ((alpha)) on cascade sizes as a function of the fraction of Simple Spreaders ((theta)). The top panels (A–C) show results when Learning Profiles are placed at random and the bottom panels (D–F) when Threshold-based Spreaders are placed preferentially in high-degree nodes. The left panels (A and D) show results for (Gamma = 0.25), the middle panels (B,E) for (Gamma = 0.50), and the right panels (C,F) for (Gamma = 0.75). Colors indicate the level of degree heterogeneity of the networks, which vary through the control parameter (alpha) used to generate the networks (see “Methods”). In that regard, Dark Blue colored lines represent lower degree heterogeneous networks (lower (alpha)) and orange higher degree heterogeneous (greater (alpha)). In each plot, the diagonal dashed line represents the identity in which an increase in the fraction of Simple Spreaders ((theta)) would lead to an equal increase in the final fraction of activated individuals (cascade size). Other parameters are (Z = 10^3) and (langle k rangle = 4). For each condition, the reported results represent the average over 1000 simulations for each of the 100 network instances, totaling (10^5) independent simulations.

Full size image

Overall, we observe different types of curves of cascade size measured in terms of the fraction of active nodes at the end of the cascading dynamics as a function of the fraction of Simple Spreaders, depending on the threshold of Threshold-based Spreaders, network structure (degree as seen in the analytical analysis and heterogeneity), and placement of individuals. For most, in the scenario of very high thresholds and high fraction of Simple Spreaders (low fraction of Threshold-based Spreaders), we generally observe a linear response regarding the cascade size as a function of the fraction of Simple Spreaders, indicating that the cascade reaches only the Simple Spreaders ((theta)). For lower thresholds, the cascade size shows some interaction between both types of individuals—cascade size is above the diagonal.

The top panel in Fig. 1 shows these curves when individuals are randomly placed in the network. For heterogeneous networks, we observe mostly concave relationships, where cascades may occur even at zero fraction of Simple Spreaders and exhibit decreasing returns on the size of the cascade as we increase the fraction of Simple Spreaders. In the case of Random Networks, there is a critical minimum fraction of Simple Spreaders for intermediate thresholds, which increases with increasing (Gamma), necessary to enable a cascade. For instance, when (Gamma = 0.25) cascades only unfold for (theta > 0.15)). After this fast growth, we recover the same growing concave response of the cascade size for increasing values of (Gamma). We refer to this as S-shaped response of the cascade curve. On closer inspection, we can see that the exponential networks already exhibit this behavior, representing a good intermediate case between random and scale-free.

Fig. 4
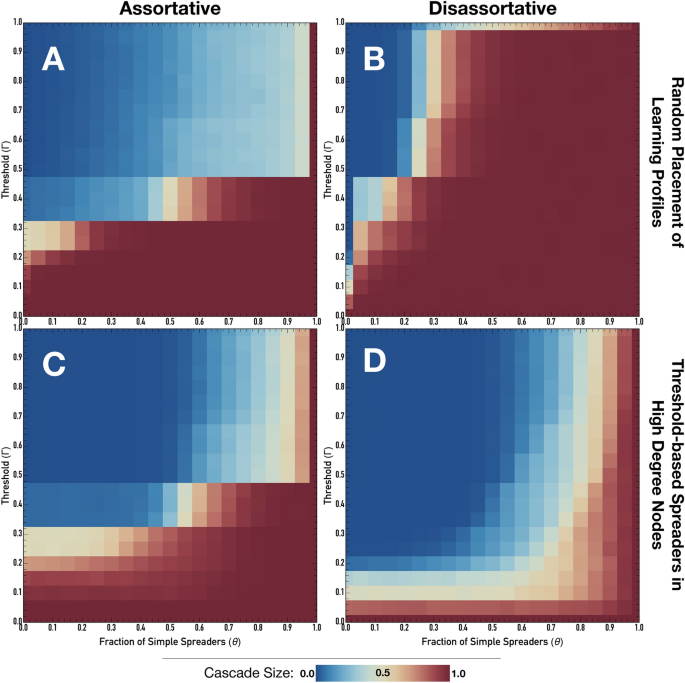
figure 4

Cascade Size as a function of Threshold-based Spreader threshold ((Gamma)) and the fraction of Simple Spreaders ((theta)) on Scale Free networks with Assortative (A,C) and Disassortative (B,D) properties and when Threshold-based Spreaders are placed at random (A,B) or assorted positively with degree (C,D). Colors indicating no cascade (blue) or full cascade (red) parameter regions. Other parameters are (Z = 10^3) and (langle k rangle = 4). For each condition, the reported results represent the average over 1000 simulations for each of the 100 network instances, totaling (10^5) independent simulations.

Full size image

Even in our baseline scenario of random placement, we can already see a rich dynamical pattern due to the interplay of the different individual learning preferences and the underlying network topologies.

Next, we look at the impact of having Threshold-based spreaders preferentially assorted in nodes with higher degrees (middle panels of Fig. 1). We place a fraction (1-theta) of Threshold-based Spreaders along nodes proportionally to their degree ((k_i)). Figure 1 D to F results compare to those of Fig. 1A–C, allowing for direct assessment of the impact of placing Threshold-based Spreaders preferentially on higher degree nodes. In this case, the cascading dynamics is characterized by the S-shape response to the fraction of Simple Spreaders ((theta)) that we saw on random networks with random placement, meaning that the cascade requires a minimum fraction of Simple Spreaders to unfold successfully. The minimal fraction increases with increasing network degree heterogeneity and (Gamma). For instance, in strongly degree heterogeneous networks, even a minority of 30% Threshold-based Spreaders can impair cascade dynamics for reasonable thresholds of (Gamma = 50%).

Instead, when Simple spreaders are preferentially assorted in nodes with a higher degree, Fig. 1 G to I, we recover the baseline behavior, albeit with some small differences. For instance, Exponential networks (Fig. 1 H) still require a critical minimum of Simple spreaders to cascade, especially for higher thresholds, similar to the results obtained for random graphs.

Overall, the suppression of the initially small cascade size with (theta) is observed when assorting Threshold-based spreaders preferentially on higher-degree nodes.

The cascade sizes depend additionally on the threshold that Threshold-based Spreaders use. Figure 2 compiles the data in Fig. 1 to more directly show how the cascade size (in red full cascade and blue no cascade) depends on the fraction of Simple Spreaders in the population ((theta)) and the threshold of Threshold-based Spreaders ((0 le Gamma le 1)). The top panels show the SFBA results and the bottom panels show Exponential networks. It becomes clear that the conditions under which it is possible to observe large cascades are limited and become narrower for increasing thresholds ((Gamma)), an outcome amplified in SFBA (high heterogeneity) compared to EXP (lower heterogeneity). Having Threshold-based Spreaders placed preferentially on high-degree nodes offers resistance to spreading and adopting information. Naturally, this can be good (if we are talking about misinformation) or bad (if we are talking about innovation).

Fig. 5
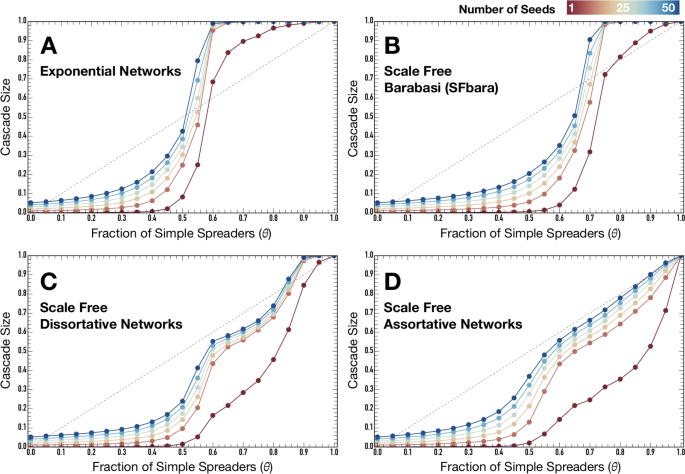
figure 5

Cascade Sizes as a function of the fraction of Simple Spreaders and different number of seeds (colors, from dark red with one seed to dark blue with 50). Each panel represents the results for different network structures: exponential graphs (A); scale-free Barabasi–Albert (B); scale-free disassortative (C); and scale-free assortative (D). The diagonal dashed line represents the identity in which an increase in the fraction of Simple Spreaders ((theta)) would lead to an equal increase in the final fraction of activated individuals (cascade size). Other parameters are (Gamma = 0.5), (Z = 10^3) and (langle k rangle = 4). For each condition, the reported results represent the average over 1000 simulations for each of the 100 network instances, totaling (10^5) independent simulations.

Full size image

From Fig. 1, it is clear that degree heterogeneity plays a role in the necessary conditions to generate an information cascade. Figure 3 explores in more detail the role of degree heterogeneity by comparing the cascade size as a function of the fraction of Simple Spreaders ((theta)) for a set of networks that interpolate low ((alpha = 1/3), dark blue) and high ((alpha = 1.0), orange) degree heterogeneity levels, which correspond to power-law degree distributed networks with different exponents (see “Methods”).

Figure 3 top panels show the results for Random Placement of Learning profiles and the bottom panels for the case when Threshold-based Spreaders occupy high-degree nodes preferentially. We consider also three different values of (Gamma = 0.25) (A and D), 0.50 (B and E), and 0.75 (C and F). Results clarify two findings. First, in the bottom panels, the critical number of SS necessary to observe a cascade when Threshold-based spreaders occupy preferentially high-degree nodes increases with increasing degree heterogeneity. This is clearly visible with the right shift that is observed in the bottom curves for all values of the (Gamma). Secondly, the role of degree heterogeneity switches from amplifying cascades when Learning profiles are randomly placed (top panels) to suppressing of cascades when Threshold-based Spreaders are placed in high-degree nodes (bottom panels). This can be seen in Fig. 3 by the change in the ordering of the colors in the curves.

Past works have highlighted the role of Assortativity mixing in cascading dynamics42,62,63, and we show it also plays a role in amplifying the previously discussed outcomes. Figure 4 shows the results obtained for assortative (panels A and C) and disassortative (panels B and D) SF networks when Threshold-based Spreaders are placed at random in the population (panels A and B) or preferentially located in higher degree nodes (panels C and D). We show that the overall dynamics of Assortative networks are relatively insensitive to the placement of Threshold-based Spreaders and usually only sensitive to the threshold of Threshold-based Spreaders ((Gamma)).

In contrast, disassortative networks show two opposite outcomes depending on the placement of Threshold-based Spreaders. First, when Threshold-based Spreaders are randomly placed, cascades typically are large for the entire range of parameters and require a minimal frequency of Simple Spreaders to unfold. Information can spread through low-degree nodes and build influence to reach hubs. Secondly, if Threshold-based Spreaders are placed preferentially on higher-degree nodes, cascades rarely unfold unless Simple Spreaders represent more than 80% of the population. In such cases, hubs mediate the diffusion of information between low-degree individuals. As such, they effectively block the diffusion of information, which faces challenges in building the necessary quorum to cascade.

So far, we have considered only the very strict scenario of a cascade starting from a single randomly placed seed. We tested different network topologies and, in particular, how the distribution of Learning Profiles leads to dramatically different outcomes. We now explore how sensitive the above results are to the number of seeds, and we focus on the case of Threshold-based Spreaders placed preferentially in higher-degree nodes. Such variation in the number of seeds naturally facilitates the cascade dynamics and can be useful to overcome the ”cold-start” problem and the barriers Threshold-based Spreaders pose. Indeed, in the literature, this is often the point of analysis. Figure 5 shows the impact of seeding up to 5% of the population (50 individuals out of 1000). We assume that seeds are placed at random.

Results show that, while increasing the number of seeds effectively increases the cascade size, and eases the conditions (e.g., critical number of Simple Spreaders), we still recover the S-shape transition—initially no or weak response, then it grows fast with (theta), then saturates—in Exponential and Scale-Free networks we identified with a single seed. A similar, although smoothed, dynamic is also present in both disassortative and assortative variants of scale-free networks, with little gains observed up to a threshold. In particular, assortative networks can never generate full cascades unless every individual is a Simple Spreader. This result contrasts with Exponential and Scale-Free networks where the presence of 50% or 70%, respectively, Simple Spreaders is a sufficient condition to generate full cascades.

Discussion

Past research has traditionally considered homogeneous populations in terms of individual adoption/learning profiles. Here, we delve into the case of a cascading dynamics process on populations that mix and controllably place Simple Spreaders and Threshold-based Spreaders. We assess how the balance of both roles and their placement on a wide range of social networks affects the cascade of novel information starting from a small number of randomly placed seeds.

We show that when both roles—Simple Spreaders and Threshold-based Spreaders—are randomly placed in a social network, they create positive synergies and result in cascades that overcome the adoption barriers of homogeneous populations of Threshold-based Spreaders. This is particularly true for degree heterogeneous networks (scale-free structures) and is somewhat more nuanced in random social structures.

However, when Threshold-based Spreaders are preferentially placed in higher-degree nodes on degree heterogeneous networks, they effectively impair the spread of information. This leads to the existence of a critical minimum number of Simple Spreaders necessary for the information to cascade. Surprisingly, these critical values are relatively large, implying that populations resist the diffusion of information that starts within the population. A dramatic outcome happens in disassortative mixing, where the mediating role of hubs completely blocks the cascade of information even when Threshold-based Spreaders have a relatively low threshold.

The implications of these results are dual and depend on whether the information being spread is socially good (e.g., innovations) or bad (e.g., misinformation). In the former case, Threshold-based Spreaders can impair the diffusion of innovations and require external intervention to facilitate transformative processes that percolate to the entire population. However, in the latter case, Simple Spreaders can represent agents placed in the social network who operate to amplify the diffusion of information and the likelihood of its virality, in particular, in contexts where a priori expectation is that information diffuses on a complex contagion scenario. In that sense, the costs do not seem to justify the means, as in many situations, well-located Threshold-based Spreaders can effectively block the cascade dynamics even in the presence of many Simple Spreaders. More importantly, it highlights the importance of having Threshold-based Spreaders influencers that operate as information filters. For practical applications, targeting high-degree nodes acting as Simple Spreaders in heterogeneous networks could suppress harmful cascades. Strategically replacing them with Threshold-based Spreaders can enhance the tunability of the spread of beneficial information. Tailoring strategies to specific network topologies, such as assortative or disassortative networks, provides a flexible toolkit for controlling cascade dynamics. For example, reducing hub connectivity or strategically placing Threshold-based Spreaders at influential positions can act as an effective barrier against misinformation. Reducing their threshold can lower that barrier. Conversely, the same interventions can inhibit the adoption of innovations, emphasizing the dual nature of these strategies.

Further exploring the role of multiple learning profiles in social systems is pertinent. Future research should revisit past paradigms in the literature on diffusion of innovations and influence maximization to benchmark how traditional seeding strategies can cope with heterogeneous populations of individuals, particularly when their distribution is structurally biased.

While our study offers valuable analytical and numerical insights, certain limitations reduce the immediate applicability of its findings to real-world networks. For instance, the empirical existence, abundance, and distribution of the different behavioral types are needed for application in specific practical settings. Similarly, the reliance on fixed-degree distributions and simplified network assumptions may overlook the complexities of real social systems, such as link dynamics, multilayered interactions, and varying connection strengths. Addressing these gaps through empirical validation, dynamic network modeling, and multilayered network representations could significantly strengthen the robustness and applicability of the results, opening pathways for future research.